Лекция 7. Исследование инвариантных к содержанию свойств предметных областей обучения

Исследование инвариантных к содержанию свойств предметных областей обучения

Проблема адаптации обучения (проблема формирования учебного задания с требуемыми свойствами) сводится к проблеме адаптации алгоритмического предписания Q к уровню обученности конкретного обучаемого на каждом шаге обучения с целью выдачи задания с мерой трудности, близкой к оптимальной.

Алгоритмическое предписание Q является как средством усвоения некоторой суммы знаний, так и предметом обучения. При выполнении задачи из рассматриваемой ПО обучения используется некоторая реализация алгоритмического предписания Q, характеризуемая используемым набором операций 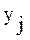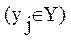, которые определяют свойства задачи.

В общем случае множество реализаций алгоритмического предписания Q можно разделить на R классов, каждый из которых характеризуется своим (уникальным) подмножеством типов операций 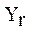(r=1,2…R), используемым для решения задач, то есть:

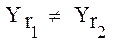(2.23)

где: ; , .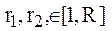

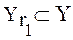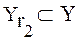В свою очередь, каждый r-й класс содержит одну или несколько реализаций алгоритмического предписания Q, где каждая реализация, принадлежащая r-му классу, описывается одним и тем же подмножеством типов используемых операций 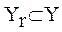. Таким образом, для однозначной идентификации конкретной реализации алгоритмического предписания требуется использовать идентификатор rq 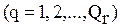, где r идентифицирует класс реализаций, а q - реализацию внутри класса. Реализаци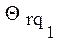и и 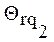, принадлежащие одному r -му классу, отличаются друг от друга тем, что описываются различными Q векторами используемых операци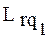й и 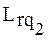, то есть:

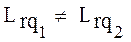(2.24)

где: .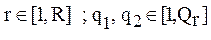

Возможность организации адаптивного обучения во многом определяется логической структурой алгоритмического предписания Q, описывающего пути решения задач в рассматриваемой ПО обучения. Анализ свойств множества реализаций 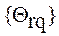позволяет выделить три следующих случая.

Множество реализаций 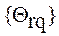состоит только из одной реализации 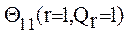, то есть все задачи соответствующей ПО обучения обладают одними и теми же свойствами, описываемыми вектором операций 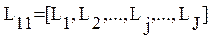, используемым для их решения. Вариативность процесса обучения может достигаться только за счет внешних, в частности, естественно-языковых форм представления задач. Задачи, обладающие одинаковыми свойствами, но отличающиеся внешней формой представления, можно считать синонимичными (задачами - синонимами). В связи с тем, что в рассматриваемом случае, процесс управления обучением представляет собой последовательную выдачу синонимичных заданий, то адаптация к обучаемому по сложности и трудности учебных заданий принципиально невозможна. Результатом применения предложенного выше метода идентификации знаний обучаемого в процессе управления обучением является индивидуально различное время достижения требуемого уровня обученности. Рассматриваемый случай характеризуется как полностью вырожденный.

Множество реализаций 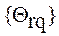состоит более чем из одной реализации, каждая из которых принадлежит к своему r-му классу 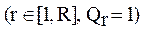, то есть каждый класс содержит ровно одну реализацию, описываемую уникальным подмножеством типов используемых операций 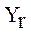и соответствующим (уникальным) вектором используемых операций .

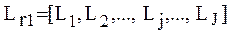Следовательно, все задачи соответствующей ПО обучения могут быть разбиты на R классов, содержащих одну или несколько синонимичных задач. Логическая последовательность выполнения задач устанавливается в этом случае экспертом - педагогом с учетом некоторых критериев сложности, рассматриваемых ниже. В соответствии с поставленной целью обучения необходимо достичь требуемого уровня обученности по каждой используемой операции, а следовательно и в каждом классе задач. Это означает, что последовательности учебных заданий, выполненные различными обучаемыми в процессе обучения, могут отличаться друг от друга числом повторений задач того или иного класса, так как переход от одного класса задач к другому регулируется уровнем обученности конкретного обучаемого. Кроме того, указанные последовательности могут отличаться друг от друга за счет использования в них синонимичных задач. Таким образом, в анализируемом случае, в целом, поддерживается принцип перехода от усвоения простого к сложному, а также принцип перехода к усвоению нового в случае успешного усвоения предыдущего. Принцип стабилизации трудности учебных заданий поддерживается частично, а именно: в случае, когда число задач в задании меньше максимально возможного и трудность задания стала меньше оптимальной, то добавлением новых задач в задание удается приблизить значение трудности задания к оптимальному или достичь оптимального. Адаптация к обучаемому заключается, в основном, в индивидуализации времени обучения. Содержательная адаптация минимальна, так как последовательности учебных заданий, выполняемые различными обучаемыми близки друг к другу, то есть рассматриваемый случай по характеру адаптации близок к линейным программам С. Пресси и характеризуется как минимально адаптивный (частично вырожденный).

В общем случае множество реализаций 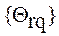состоит из R классов реализаций и существуют такие классы, которые, в свою очередь,

содержат более одной реализации 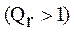. Каждая из реализаций, принадлежащая одному r -му классу, описывается одним и тем же подмножеством типов используемых операций 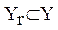и соответствующим (уникальным) вектором используемых операций L_rq = [L ₁, L ₂, …, L_j, L_J].

Следовательно, все задачи рассматриваемой ПО обучения могут быть разбиты на R соответствующих классов. Кроме того, существуют такие классы задач, в которых могут быть выделены 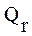подклассов, содержащих наборы синонимичных задач. Свойства каждой из задачи указанного подкласса описываются вектором операций L_rq, используемым для их решения.

Для реализации принципа усвоения от простого к сложному требуется упорядочить задачи рассматриваемой ПО обучения по сложности. Предложенная ранее количественная оценка сложности учебного задания (2.2) соответствует ее понятийному определению. В то же время, учитывая, что выделенный экспертом-педагогом состав операций, входящих в алгоритмическое предписание, устойчив и объективен лишь относительно, также относительна, в смысле адекватности, и предложенная количественная оценка сложности.

Введение в количественную оценку сложности весовых коэффициентов 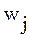, учитывающих разнотипность (неоднородность) используемых при выполнении задания операций (в этом случае 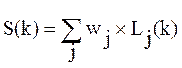), также не исчерпывает проблему адекватности оценки сложности, а главное, предложенные количественные оценки не могут служить единственным критерием упорядочивания задач ПО обучения, т. к. это может привести к разрушению уже существующих и (или) вводимых логических связей между задачами ПО обучения (например, к разрушению введенному разбиению на классы и подклассы). В связи с этим вводится рассматриваемая ниже двухшаговая процедура упорядочивания задач ПО обучения.

На первом шаге осуществляется "упорядочивание по классам", которое заключается в следующем.

При наличии логических связей, определяющих порядок освоения классов учебных задач, соответствующий критерий обладает наивысшим приоритетом в процедуре упорядочивания. При отсутствии явных логических связей, порядок может определяться исходя из существующих традиций организации обучения в рассматриваемой ПО, а так же опыта и интуиции эксперта-педагога. В случае, когда отсутствуют явные логические связи и устоявшиеся традиции, определяющие порядок, целесообразно использовать некоторый критерий, основанный на количественных оценках сложности r -го класса учебных задач 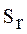. В качестве примеров оценок сложности можно привести следующие.

Сложность r -го класса задач 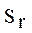оценивается по сложности некоторой произвольно выбранной задачи в рассматриваемом классе:

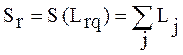(2.25)

где: 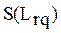- сложность вектора операций 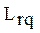, используемого при решении выбранной задачи ;

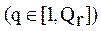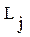- число операций типа j, входящих в вектор .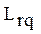

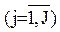Сложность r -го класса задач 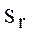оценивается по суммарной сложности задач, входящих в класс, за исключением синонимичных:

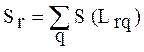(2.26)

где: .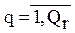

Сложность r-го класса задач 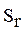оценивается по усредненной

сложности нескольких разнотипных задач, входящих в класс:

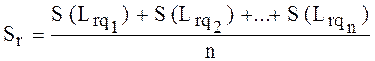(2.27)

где: q ₁, q ₂,…, q_n Î [1, Q_r] и .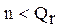

При 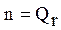формулу (2.27) можно представить в виде:

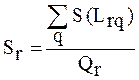(2.28)

где: .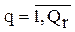

То есть, в этом случае сложность r -го класса задач 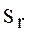оценивается по усредненной сложности всех типов задач, входящих в класс.

Предложенные количественные оценки сложности носят статический характер (отчуждены от динамики усвоения). В то же время, в соответствии с теорией поэтапного формирования умственных действий, в процессе обучения происходит "свертываемость" выполняемых операций по мере роста уровня обученности. Таким образом, при "упорядочивании по классам", необходимо учитывать "близость" классов по типам используемых операций, то есть учитывать эффект " свертываемости" операций, когда:

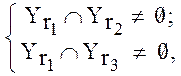(2.29)

где: r ₁, r ₂, r ₃ Î [1, R];

;

;

.

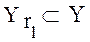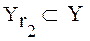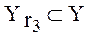В этом случае также могут вводится разнообразные количественные оценки "близости". Например, оценка "близости" к r ₁ -му классу учебных задач может зависеть от значений математического ожидания числа ошибок, которые могут быть допущены при решении задач, принадлежащих r ₂ -му и r ₃ -му классам, при условии, что решение задач, принадлежащих r ₁ -му классу будет осуществляться раньше.

Вторым шагом процедуры упорядочивания задач ПО обучения является "упорядочивание внутри класса".

Рассматривается множество реализаций алгоритмического предписания Q, принадлежащих r-му классу: 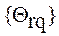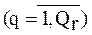. Каждая из указанных реализаций характеризуется одним и тем же подмножеством типов используемых операций 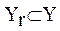, но различными векторами 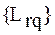. Среди указанного множества векторов 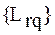выбираются вектора минимальной и максимальной сложности, вычисляемой по формуле (2.2). Выбранным векторам присваиваются соответственно идентификаторы r1 и . Введенное определение минимальной и максимальной сложности корректно, если для всех j выполняются соответствующие неравенства:

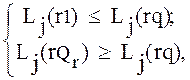(2.30)

где: 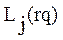-j-ый компонент вектора ;

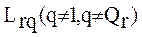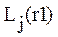- j-ый компонент вектора минимальной сложности ;

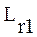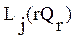- j-ый компонент вектора максимальной сложности .

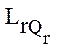В противном случае определение минимальной и максимальной сложности ограниченно корректно, так как приходится сравнивать между собой операции различных типов и тогда эксперт-педагог может определить другие вектора в качестве минимально и максимально сложных. Важным является само выделение таких векторов, так как, если процесс обучения в r-м классе будет начинаться с решения задач, свойства которых описываются вектором 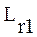, и заканчиваются решением задач, свойства которых описываются вектором 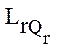, то будет реализован дидактический принцип "от простого к сложному".

Упорядочивание оставшихся векторов 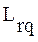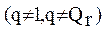между минимально и максимально сложными произвольно. Это связано с тем, что реализаци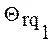и и 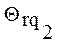считаются изоморфными, если соответствующие им вектора 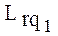и 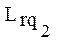связаны между собой следующей зависимостью. Для всех j имеет место:

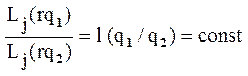(2.31)

где: 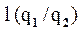- коэффициент, характеризующий сложность вектора 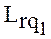, относительно сложности вектора .

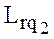Таким образом, если все реализации алгоритмического предписания Q, принадлежащие r-му классу изоморфны относительно друг друга (соотношение (2.31) выполняется для всех 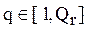), то соответствующие им вектора 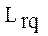могут быть строго упорядочены по сложности, но при этом учебные задачи, чьи свойства они описывают, будут обладать для конкретного обучаемого на конкретном шаге обучения одной и той же трудностью (в соответствии с ее определением (2.3)), что интуитивно ясно, так как в них будет одно и то же соотношение "плохо" и "хорошо" усвоенных операций. Следовательно, адаптация по трудности к обучаемому в этом случае принципиально невозможна. То есть, чем меньше r-ый класс содержит изоморфных реализаций, тем разнообразнее свойства соответствующего ему множества учебных задач с точки зрения значений их трудности для конкретного обучаемого на конкретном шаге обучения, а следовательно и выше потенциальная возможность найти для указанного обучаемого оптимальную (из имеющихся) по трудности учебную задачу. 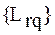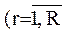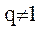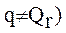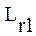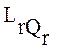При соблюдении указанных условий объединение подмножеств векторов , , определяет область возможной адаптации управления обучением по трудности учебных задач, а совокупность векторов и позволяет реализовать дидактический принцип "от простого к сложному".

Рассмотренные свойства множества реализаций алгоритмического предписания 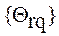инвариантны к содержанию ПО обучения и могут считаться универсальными при условии, что эксперт-педагог согласен с дидактическими принципами организации обучения, приведенными выше, и их формализацей в модели обучения.

Вопросы для самоконтроля

1. Чем определяется возможность организации адаптивного обучения?

2. В чем заключается адаптация к обучаемому?

3. Что требуется для реализации принципа усвоения от простого к сложному?

4. В чем заключается смысл "упорядочивания по классам"?

5. Что надо учитывать при "упорядочивании по классам"?

6. Как называется второй шаг процедуры упорядочивания задач ПО?

Дата добавления: 2014-01-13