
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 8. Определение свойств формируемого задания
|
|
|
|
Определение свойств формируемого задания
Анализ свойств ПО обучения, инвариантных к содержанию, показал ограниченную адекватность предложенной формализации понятия сложности учебной задачи и соответственно учебного задания, которое может состоять из одной или нескольких разнотипных задач. Выявлен относительный характер указанной формализации, иллюстрируемой системой неравенств (2.30).
Формализация понятия трудность учебного задания (задачи) представляют собой еще большую проблему, так как приводимые естественно-языковые определения характеризуются очень высоким уровнем размытости, нечеткости. Из приводимых определений можно сделать следующие выводы:
§ трудность задания с одной стороны характеризует его объективные свойства, с другой - свойства обучаемого (уровень знаний обучаемого), то есть относится не только к заданию, но и к процессу его выполнения конкретным обучаемым;
§ трудность задания определяется субъективной степенью новизны предлагаемого для усвоения учебного материала, то есть при алгоритмическом подходе к процессу обучения должна учитываться степень неусвоенности операций, используемых для выполнения задания;
§ одно и то же задание обладает различной мерой трудности для различных обучаемых (низкой - для "успевающего" обучаемого, высокой - для "неуспевающего").
Наконец, в процессе обучения, должен соблюдаться принцип стабилизации трудности последовательно выдаваемых учебных заданий, сформулированный И.М.Сеченовым.
Одной из числовых оценок процесса обучения, удовлетворяющей приведенным требованиям, кроме требования возможности стабилизации, является математическое ожидание числа ошибок при выполнении задания MAT(k), вычисляемое по формуле (2.4).
Требование стабилизации значений указанной оценки не выполнимо в общем случае, так как область допустимых значений MAT(k) зависит от сложности задания S(k) и определяется в рассматриваемой модели следующим образом:
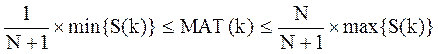 (2.32)
(2.32)
где: N - число гипотез о состояниях обученности (используется для пересчета значений  по результатам шага обучения с использованием формулы Бейеса).
по результатам шага обучения с использованием формулы Бейеса).
Из (2.32) следует, что стабилизация значений MAT(k) возможна только в случае наложения ограничений на область допустимых значений 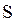 (k). Это не приемлемо в общем случае, так как существенно ограничивает область применения модели.
(k). Это не приемлемо в общем случае, так как существенно ограничивает область применения модели.
На понятийном уровне MAT(k) можно интерпретировать как количественную оценку объема трудозатрат обучаемого при выполнении задания (оценку трудоемкости задания).
Действительно MAT(k) отражает следующие закономерности:
§ увеличение сложности любого компонента задания (и соответственно значения 
 ) ведет к увеличению трудоемкости задания для любого обучаемого и наоборот;
) ведет к увеличению трудоемкости задания для любого обучаемого и наоборот;
§ трудоемкость конкретного задания выше для "неуспевающего" обучаемого и ниже для "успевающего".
Предложенная выше (формула (2.3)) формализация понятия меры трудности учебного задания полностью удовлетворяет приведенным выше требованиям, в том числе и требованию возможности стабилизации ее значений.
Область допустимых значений T(k) не зависит от S(k), что обеспечивает возможность стабилизации указанных значений. Эта область определяется следующим образом:
 (2.33)
(2.33)
Таким образом, стабилизация меры трудности учебных заданий означает стабилизацию доли неусвоенного материала в общем объеме всего материала, предъявляемого обучаемому для усвоения на каждом шаге обучения. Естественно, что по содержанию, в зависимости от того, операции каких типов усвоены хуже, указанная доля уникальна для каждого обучаемого. То есть, учебное задание для конкретного обучаемого на каждом шаге обучения содержит те компоненты изучаемого предмета, которые недостаточно им усвоены. Следовательно достигается содержательная адаптация процесса обучения к конкретному обучаемому, что и обуславливает индивидуальную минимизацию времени обучения.
В качестве характерных свойств T(k), как количественной оценки задания, отличной от MAT(k), можно указать следующее:
§ увеличение сложности любого компонента задания не приводит к однозначному увеличению трудности задания (трудность может увеличиться, уменьшиться или остаться прежней) и наоборот;
§ в случае, когда учебный материал усваивается обучаемым "равномерно" (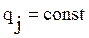 для всех j) трудность задания не зависит от его сложности (в этом случае
для всех j) трудность задания не зависит от его сложности (в этом случае 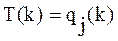 );
);
§ изменение трудности задания возможно лишь в случае "неравномерного" усвоения учебного материала (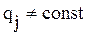 для всех
для всех 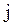 );
);
§ изменение трудности задания, при "неравномерном" усвоении учебного материала, вызывается изменением его сложности и (или) трудоемкости.
Существует два основных, противоположных подхода к изменению трудности, как доли неусвоенного материала задания:
§ уменьшение (увеличение) доли неусвоенного материала осуществляется только за счет уменьшения (увеличения) объема неусвоенного материала в общем объеме учебного материала задания;
§ уменьшение (увеличение) доли неусвоенного материала осуществляется только за счет увеличения (уменьшения) объема усвоенного материала в общем объеме учебного материала задания.
Естественно, в общем случае, возможна комбинация указанных подходов.
Для обеспечения интеллектуальности ("разумности") управления процессом обучения в целом, требуется оценить "разумность" каждого из указанных подходов к изменению трудности задания и определить условия их применения. В первом подходе уменьшение (увеличение) трудности задания осуществляется при уменьшении (увеличении) его сложности и трудоемкости, что соответствует интуитивному представлению об интеллектуальности управления мерой трудности. Во втором подходе уменьшение (увеличение) трудности задания осуществляется при увеличении (уменьшении) его сложности и трудоемкости, что противоречит здравому смыслу, так как естественной причиной уменьшения (увеличения) трудности задания является "низкий" ("высокий") уровень знаний обучаемого. Следовательно, в алгоритме стабилизации меры трудности должны быть предусмотрены дополнительные ограничения, которые снимали бы указанные противоречия в общем случае (в том числе и в случае комбинации двух подходов к изменению трудности задания).
В качестве требуемых ограничений целесообразно использовать значение трудоемкости задания, как более полной (адекватной), по сравнению со сложностью задания, оценкой трудозатрат обучаемого при выполнении задания. Таким образом, при управлении значением трудности задания должны соблюдаться следующие правила:
§ уменьшение трудности задания не должно сопровождаться увеличением его трудоемкости даже в случае увеличения его сложности;
§ увеличение трудности задания не должно сопровождаться уменьшением его трудоемкости даже в случае уменьшения его сложности.
С учетом введенных ограничений алгоритм стабилизации меры трудности учебных заданий можно представить в виде следующей последовательности шагов. Необходимо отметить, что описываемые ниже шаги алгоритма стабилизации трудности осуществляются для каждого класса задач, по которому на k-м шаге обучения принимается решение продолжить обучение.
Шаг 1. По результатам k-го шага обучения определяются значения 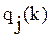 для всех j.
для всех j.
Шаг 2. Прогнозируются значения  на (k+1)-й шаг обучения:
на (k+1)-й шаг обучения:  .
.
Шаг 3. В рассматриваемом классе задач пересчитывается прогнозируемое на (k+1)-й шаг обучения значение трудности задач того же типа 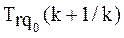 , что и на предыдущем шаге. Если выполняется условие:
, что и на предыдущем шаге. Если выполняется условие:
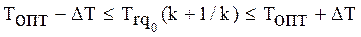 (2.34)
(2.34)
то задача указанного типа вновь включается в учебное задание, формируемое на (k+1)-й шаг обучения.
Шаг 4. Если условие (2.34) не выполняется, то для всех типов задач рассматриваемого класса вычисляются отклонения их значений трудности от оптимального:
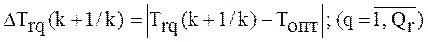 (2.35)
(2.35)
Шаг 5. Если требуется уменьшить трудность (рис. 2.3), то есть имеет место:
 (2.36)
(2.36)
то в рассматриваемом классе осуществляется поиск задач такого типа, трудность которых 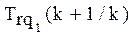 имела бы минимально возможное отклонение от оптимальной:
имела бы минимально возможное отклонение от оптимальной:
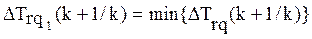 ;
;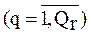 (2.37)
(2.37)
При этом трудоемкость задач искомого типа не должна возрастать, то есть:
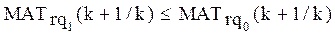 (2.38)
(2.38)
Кроме того, если для задач различных типов имеет место симметричное отклонение их значений трудности от оптимального:
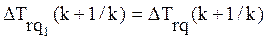 ;
;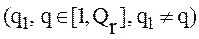 (2.39)
(2.39)
то в задание, формируемое на (k+1)-й шаг обучения, включается задача
При 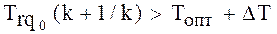

Направление поиска

Соблюдаемое ограничение:
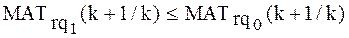
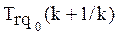
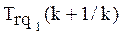
 |  |






 0([ ])1
0([ ])1
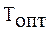
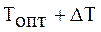
Рис. 2.3 Уменьшение меры трудности учебного задания.
такого типа, значение трудности которой ближе к значению 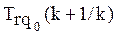 , то есть для которой, в рассматриваемом случае, дополнительно выполняется:
, то есть для которой, в рассматриваемом случае, дополнительно выполняется:
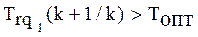 (2.40)
(2.40)
В противоположном случае, когда требуется увеличить трудность (рис. 2.4), то есть имеет место:
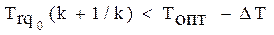 (2.41)
(2.41)
используется тот же критерий поиска (2.37). При этом должны соблюдаться противоположные ограничения.
Трудоемкость задач искомого типа не должна уменьшаться, то есть:
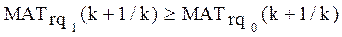 (2.42)
(2.42)
Если имеет место симметрия отклонения трудностей (2.39), то дополнительно должно выполняться (рис. 2.5):
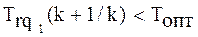 (2.43)
(2.43)
В заключение необходимо отметить следующее. Естественно-языковые определения психолого-педагогических понятий, в частности: сложности и трудности учебного задания характеризуются высоким уровнем неопределенности. Формализация указанных понятий представляет собой актуальную проблему, решение которой позволяет перейти к автоматизации функции управления процессом обучения в экспертных обучающих системах (ЭОС). Качество формализации (ее адекватность) во многом определяет уровень интеллекта ЭОС. В результате проведенных исследований в алгоритм стабилизации меры трудности учебных заданий введен ряд ограничений, исключающих принятие решений, противоречащих здравому смыслу. В основу указанных ограничений положены формализованное понятие трудоемкости учебного задания и учет предыстории обучения.
При 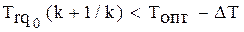
 |
Направление поиска

Соблюдаемое ограничение:
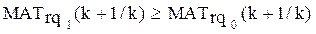
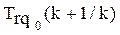
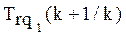



 1([ | ])0
1([ | ])0
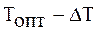
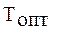
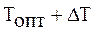
Рис. 2.4 Увеличение меры трудности учебного задания
 При При 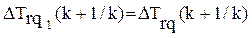 , где , где 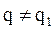
|
 |
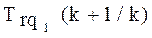 |
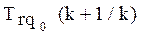
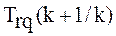
 | |||
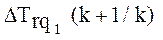 | |||

 ([ ])
([ ])
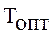
|

|
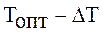
|
Рис. 2.5 Симметричное отклонение мер трудностей учебных заданий.
Вопросы для самоконтроля
1. Что показал анализ свойств ПО обучения?
2. Что характеризует трудность задания?
3. Какой принцип должен соблюдаться в процессе обучения?
4. Назовите два основные противоположные подходы к изменению трудности материала задания?
5. Назовите правила, которые должны соблюдаться при управлении значением трудности задания?
6. Что требуется для обеспечения интеллектуальности ("разумности") управления процессом обучения?
7. Что означает стабилизация меры трудности учебных заданий?
8. От чего зависит и как определяется область допустимых значений 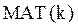 ?
?
9. В виде каких последовательностей шагов можно представить меры трудности учебных заданий?
10. Кем сформирован принцип стабилизации трудности последовательно выдаваемых учебных заданий
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 428; Нарушение авторских прав?; Мы поможем в написании вашей работы!