
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм поиска оптимального параметра системы стимулирования
|
|
|
|
1.С помощью метода Ньютона решается оптимизационная задача для центра (3.3). Задаются начальные приближения для параметра системы стимулирования 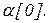
2.В точке  вычисляются первая и вторая производные целевой функции центра по приближённым формулам:
вычисляются первая и вторая производные целевой функции центра по приближённым формулам:

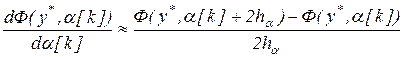 , (3.5)
, (3.5)
 (3.6)
(3.6)
где  - приращение параметра
- приращение параметра 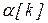 на k-й итерации.
на k-й итерации.
Для численного дифференцирования по формулам (3.5)-(3.6) необходимо вычислять значение целевой функции центра 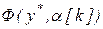 в трёх точках
в трёх точках 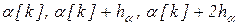 . Целевая функция центра зависит от параметра системы стимулирования
. Целевая функция центра зависит от параметра системы стимулирования 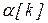 и реакции агента y. Для определения реакции агента y* на k итерации необходимо решить оптимизационную задачу (3.4). Для решения оптимизационной задачи агента также используется метод Ньютона (пункты 2.1-2.3). После нахождения первой и второй производных целевой функции центра осуществляется переход к пункту 3.
и реакции агента y. Для определения реакции агента y* на k итерации необходимо решить оптимизационную задачу (3.4). Для решения оптимизационной задачи агента также используется метод Ньютона (пункты 2.1-2.3). После нахождения первой и второй производных целевой функции центра осуществляется переход к пункту 3.
Алгоритм поиска реакции агента при заданном параметре 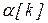 .
.
2.1.Задаются начальные приближения для реакции агента  .
.
2.2.В точке 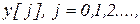 вычисляются первая и вторая производные функции агента.
вычисляются первая и вторая производные функции агента.
Для численного дифференцирования целевой функции агента используются следующие приближенные формулы:
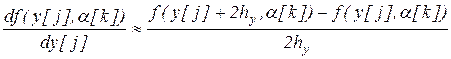 ,
,
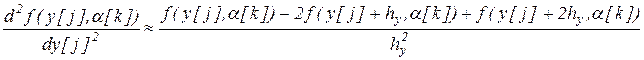 где
где  - приращение для реакции агента
- приращение для реакции агента  на j-ой итерации.
на j-ой итерации.
2.3.На каждой j-ой итерации поиска реакции агента вычисляются значения  при известном параметре системы стимулирования
при известном параметре системы стимулирования 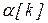 в соответствии с методом Ньютона:
в соответствии с методом Ньютона:
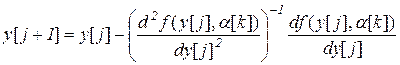 .
.
2.4.Проверяется условие выхода из итерационного процесса
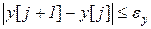 .
.
где 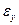 - заданная малая величина для итерационного процесса поиска реакции агента y*.
- заданная малая величина для итерационного процесса поиска реакции агента y*.
Если условие выполняется, то итерационный процесс прекращается, в противном случае осуществляется переход к пункту 2.2. В случае останова итерационного процесса и успешного определения реакции агента y осуществляется возврат к пункту 2.
3.На каждой k-й итерации поиска параметра системы стимулирования вычисляется новое значение параметра 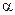 в соответствии с методом Ньютона:
в соответствии с методом Ньютона:
 .
.
4.Проверяется условие выхода из итерационного процесса поиска параметра системы стимулирования:
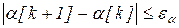 ,
,
где  - заданная малая величина для итерационного процесса поиска параметра
- заданная малая величина для итерационного процесса поиска параметра  .
.
Если условие выполняется, то итерационный процесс прекращается, в противном случае осуществляется переход к пункту 2.
Пример 3.1. Задача стимулирования для одноэлементной системы
Руководитель поручает рабочему производство продукции, используя следующую систему стимулирования:  , где α – ставка оплаты единицы произведенной агентом продукции. Цена, по которой центр продаёт продукцию, p=1000 руб. Затраты агента, выраженные в денежной форме:
, где α – ставка оплаты единицы произведенной агентом продукции. Цена, по которой центр продаёт продукцию, p=1000 руб. Затраты агента, выраженные в денежной форме: 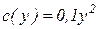 . Определитьпараметр системы стимулирования α.
. Определитьпараметр системы стимулирования α.
Решение:
Запишем целевую функцию центра: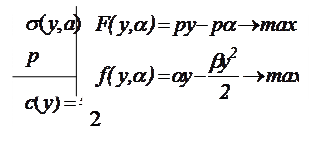
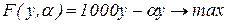
и целевую функцию агента:
 .
.
Задача стимулирования формулируется:

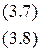
Первый этап. Найдем реакцию агента из решения оптимизационной задачи (3.8). Для этого продифференцируем выражение (3.8) по y и приравняем к нулю:
 .
.
Решая уравнение, определим реакцию агента:
 .
.
Второй этап. Подставим реакцию агента в целевую функцию (3.7):
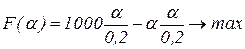 .
.
Вычислим первую производную и приравняем к нулю:
 .
.
Решая уравнение, определим параметр α:
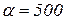 .
.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 635; Нарушение авторских прав?; Мы поможем в написании вашей работы!