Исследование механизмов стимулирования в многоэлементных системах со слабосвязанными агентами

Системы, в которых вознаграждение и затраты каждого агента зависят от действий всех агентов, называются системами с сильно связанными агентами.

Cформируем задачу стимулирования для системы со слабо связанными агентами:

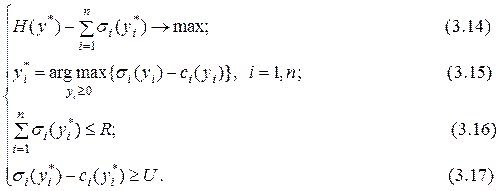
Условие (3.14) учитывает ограниченность фонда заработной платы R. Данная задача решается в два этапа. На первом этапе из выражения (3.15) определяется действие агента как аналитическая зависимость от параметров системы стимулирования центра. На втором этапе полученная аналитическая зависимость подставляется в формулу (3.14), таким образом, получается задача условной оптимизации. Решая эту задачу методом Лагранжа, определяют параметры системы стимулирования.

Рассмотрим задачу стимулирования с квадратичной функцией затрат агентов и пропорциональной системой стимулирования. Руководитель (центр) поручает работу бригаде, состоящей из n -агентов. Центр использует пропорциональную систему стимулирования: 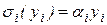, где 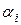– ставка оплаты единицы произведенной i -м агентом продукции. Известна функция затрат каждого агента: 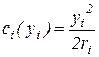, где 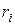– коэффициент, который характеризует квалификацию i –го агента и переводит затраты в денежное выражение. Чем выше квалификация агента, тем меньше его усилия по производству продукции. Известна рыночная цена, по которой продается продукция р, фонд заработной платы бригады R. Требуется определить параметры системы стимулирования 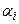. Сформулируем задачу стимулирования:

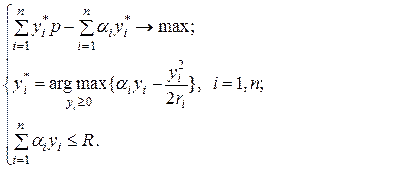
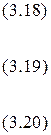
Первый этап. Из выражения (3.19) определим реакцию агента. Для нахождения экстремума функции одной переменной продифференцируем функцию и приравняем к нулю:

.

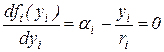Из решения уравнения следует 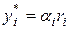. Стратегия агента по сравнению с одноэлементной задачей не изменилась. Объем произведенной продукции i -го агента прямо пропорционален ставке оплаты единицы продукции 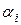и квалификации .

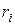Второй этап. Подставим 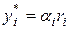в выражение для целевой функции центра (3.18) и ограничение (3.19), получим задачу на условный экстремум:

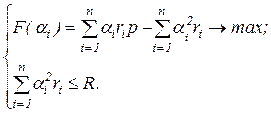
Для ее решения применим метод множителей Лагранжа. Запишем функцию Лагранжа: .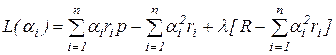

Найдём частные производные от функции Лагранжа по неизвестным:

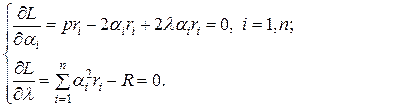
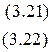
Вынесем в выражении (3.21) общий множитель за скобки:

.

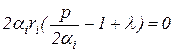Два множителя равны нулю, когда хотя бы один из них равен нулю. Первый множитель не может быть равен нулю из экономического смысла. Значит, нулю равен второй множитель:

.

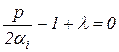Решая уравнение, получаем

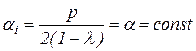. (3.23)

Получилось, что параметры функций стимулирования для всех агентов одинаковы. Из ограничения (3.22) определяем параметр системы стимулирования:

.

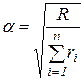Ставка оплаты единицы продукции прямо пропорциональна фонду заработной платы и обратно пропорциональна сумме квалификаций агентов. Система стимулирования, в которой зависимость вознаграждения от действий агентов одинакова, называется унифицированной.

Пример 3.2. Задача стимулирования со слабо связанными агентами

Руководитель поручает работу бригаде, состоящей из двух рабочих. Центр использует пропорциональную систему стимулирования: 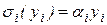, где 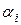– ставка оплаты единицы произведенной i -м агентом продукции. Известна функция затрат каждого агента: 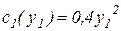, 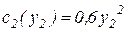. Рыночная цена, по которой продается продукция р= 1000 руб., фонд заработной платы бригады R=2 0000 руб. Определить параметры системы стимулирования α₁ и α₂.

Решение. Сформулируем задачу стимулирования:

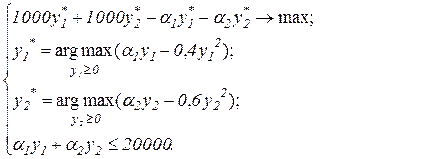
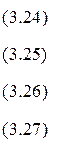
Первый этап. Из выражения (3.25) и (3.26) определим реакцию агентов. Для нахождения экстремума функции одной переменной продифференцируем функции и приравняем к нулю:

, .

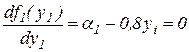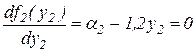Из решения уравнений следует , .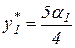

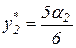Второй этап. Подставив 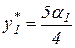и 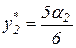в выражение для целевой функции центра (3.24) и ограничение (3.27), получим задачу на условный экстремум:

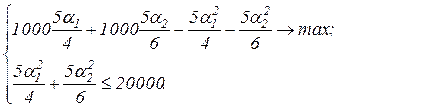
Для ее решения применим метод множителей Лагранжа. Запишем функцию Лагранжа:

.

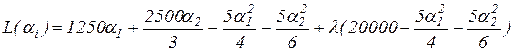Найдём частные производные от функции Лагранжа по неизвестным 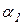, 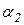и :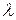

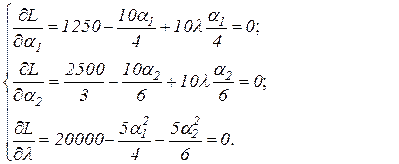
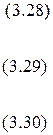
Выразим из (3.28) и (3.29) неизвестные , :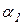

.

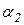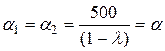Получилось, что параметры функций стимулирования для обоих агентов одинаковы. Из ограничения (3.30) определяем параметр системы стимулирования:

.

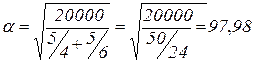Данная система стимулирования является унифицированной.

Дата добавления: 2014-01-13