Математические модели принятия решений участниками производственной системы

Несовпадение экономических интересов участников производственной системы происходит из-за разных требований, предъявляемых заказчиком и поставщиками к объёмам, срокам поставки, качеству комплектующих и др.

Для исследований процессов взаимодействия участников производственной системы сформулируем модель принятия решений поставщиками и заказчиком для определения оптимального объёма поставки комплектующих.

В качестве целевой функции поставщиков рассматривается максимизация прибыли. Целевые функции поставщиков запишутся:

, (4.1)

где 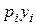- выручка от продажи комплектующих, 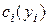- затраты i -го поставщика на производство комплектующих, включающая стоимость сырья и материалов, выплату заработной платы и налогов и др.

В практической деятельности фирм часто затраты представляют собой квадратичную зависимость от объёма выпуска комплектующих:

(4.2)

где - коэффициенты функции затрат.

С учётом выражения для затрат (4.1) целевая функция (4.2) запишется:

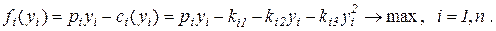
Поставщики не могут производить комплектующих больше, чем максимально возможный объём, из-за ограниченности производственных мощностей:

.

Тогда модель принятия решений для поставщиков запишется:

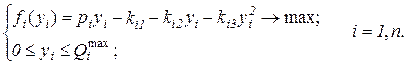(4.3)

Оптимальным решением модели (4.3) является:

,

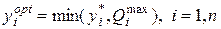где 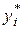- объём выпуска комплектующих i -ым поставщиком, максимизирующий прибыль.

Для нахождения 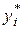продифференцируем целевую функцию по 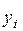и приравняем нулю:

,

.

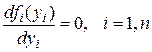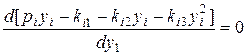Для первого поставщика получим уравнение:

,

Решая уравнение, найдём объём выпуска комплектующих поставщиками, который максимизирует прибыль:

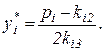
Определим оптимальный объём выпуска комплектующих, с учётом ограничений:

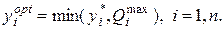(4.4)

Количество готовых изделий, которые можно собрать из этого количества комплектующих:

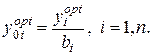
В качестве целевой функции заказчика рассмотрим максимизацию прибыли:

.

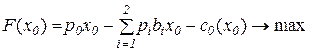где 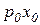- выручка от продажи готовых изделий; - затраты на покупку комплектующих, 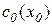- затраты заказчика на сборку готового изделия.

Затраты заказчика на сборку готового изделия представляют собой квадратичную зависимость от объёма выпуска готовой продукции:

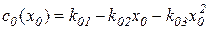, (4.5)

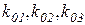- - коэффициенты функции затрат заказчика.

С учётом выражения для затрат (4.5) целевая функция заказчика запишется:

.

На объём выпуска готовых изделий наложено ограничение, связанное с невозможностью или нецелесообразностью производить выпуск готовых изделий больше, чем максимально возможный объём выпуска или спрос на изделия :

.

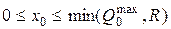Модель принятия решений для заказчика примет вид:

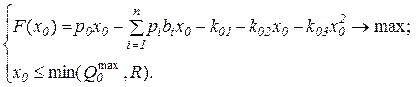(4.6)

Оптимальным решением модели (4.6) является:

, (4.7)

где 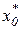- объём выпуска изделий заказчиком, максимизирующий прибыль.

Для нахождения 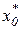продифференцируем целевую функцию по и приравняем нулю:

.

Решая данное уравнение, получим:

Учитывая ограничение, определим оптимальный объём выпуска готовых изделий .

Дата добавления: 2014-01-13