Основные понятия теории графов

Исторически теория графов, как самостоятельное научное направление возникла из задачи о семи кенигсбергских мостах, соединяющих берега и два острова на реке Преголи (рис. 12.1).

Рис. 12.1

Можно ли пройти по всем семи мостам, не проходя ни по одному из них дважды?

Граф для задачи выглядит следующим образом (рис. 12.2):

Рис. 12.2

Здесь: 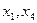– берега реки; 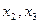– острова; линии, соединяющие точки – мосты.

Отрицательное решение этой задачи в 1736г. получено Эйлером. Со временем, результаты теории графов стали находить все более широкое применение, в том числе для решения экономических задач.

Определение 12.1. Теория графов – это раздел математики, основной особенностью которого является геометрический подход к изучению объектов.

Основным объектом теории графов является граф, который определяется заданием двух конечных дискретных множеств:

1) множество вершин ;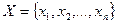

2) множество линий связи между ними .

Линии связи называются ребрами, если не указана их ориентация; если же задано направление связи, то - дугами.

Граф, состоящий из дуг, называется ориентированным графом (орграфом), а образованный ребрами – неориентированным.

Например, 1) ориентированный граф (рис. 12.3)

Рис. 12.3

2) неориентированный граф (рис 12.4)

Рис. 12.4

Вершины 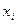и 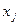, связанные дугой/ребром 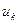, называются концевыми вершинами этой дуги/ребра. Если концевые вершины совпадают, то дугу/ребро называют петлей. Дуги/ребра с одинаковыми концевыми вершинами называются параллельными. Граф без петель и параллельных линий связи называется простым. Концевые вершины одной дуги/ребра или дуги с общей вершиной называются смежными. Простой граф, в котором каждая пара вершин смежна называется полным. Ребро/дугу называют инцидентным вершине, если оно соединено с ней.

Вывод: смежность – это отношение связности между однородными элементами (вершинами или дугами/ребрами), а инцидентность – между разнородными.

Вершина, не имеющая отношений смежности, называется изолированной. Графы с одинаковым отношением инцидентности, называются изоморфными и отличаются друг от друга только геометрической конфигурацией.

Примеры. На рисунке 12.5 представлены изоморфные графы:

Рис. 12.5.а

Рис. 12.5.б

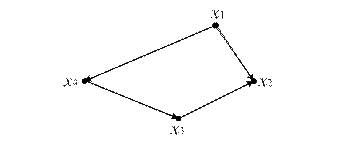
Рис. 12.5.в

Степенью P (x_i) вершины x_i называется число дуг/ребер графа, инцидентных данной вершине.

В орграфе без петель различают полустепени захода P⁺ (x_i) вершины x_i – количество дуг, входящих в x_i, и полустепени исхода P^– (x_i) – количество дуг, исходящих из вершины x_i. Понятно, что P⁺ (x_i)+P^– (x_i) =P (x_i).

В различных приложениях теории графов дугам/ребрам графов, моделирующим реальные процессы, ставят в соответствие числовые характеристики: (длина пути, время выполнения работы, пропускная способность), называемые весом дуг/ребер. В таких случаях граф называют взвешенным.

Путем в орграфе называется последовательность дуг, в которой конец любой предыдущей дуги совпадает с началом следующей. Путь, проходящий через все вершины, и притом только по одному разу, называют гамильтоновым. Путь, содержащий все дуги графа, и притом только по одному разу, называют эйлеровым. Конечный путь, у которого начальная вершина совпадает с конечной, называют контуром. Контур, проходящий через каждую вершину графа только по одному разу (за исключением начальной и конечной вершин), называют гамильтоновым.

В неориентированном графе путь называют цепью, контур – циклом. Орграф/неориентированный граф называют связным, если каждые две его вершины можно соединить путем/цепью. Орграф называют сильно связным, если между любыми двумя его вершинами существует хотя бы один путь.

Пример. а) Сильно связный граф (рис. 12.6.а)

Рис. 12.6.а

б) Несвязный граф (рис. 12.6.б)

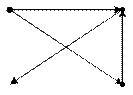
Рис. 12.6.б

Примерами графов могут служить схемы железных или шоссейных дорог, схемы связи поставщиков и потребителей, структурные формулы молекул и т.д.

Дата добавления: 2014-01-13