Потоки на сетях. Постановка задачи о максимальном потоке

Матричные способы задания графов. Упорядочение элементов орграфа

При большом числе элементов рисунок графа теряет наглядность. В таком случае граф целесообразно задать матричным способом. Этот способ также удобен и для решения задачи на компьютере.

Определение 12.3. Матрицей инцидентности орграфа без петель с n вершинами и m дугами называется матрица, любой элемент которой определяется по следующей формуле:

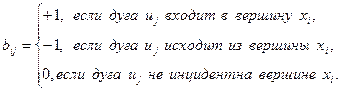
Для неориентированного графа вместо «–1» ставится «1».

Пример. Для заданного ориентированного графа (рис. 12.10) построить матрицу инцидентности:

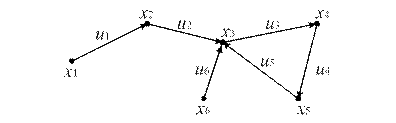
Рис. 12.10

Матрица инцидентности орграфа:

.

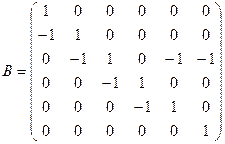Определение 12.4. Матрица смежности вершин орграфа – квадратная матрица n -го порядка (n – число вершин). Строки и столбцы матрицы соответствуют вершинам графа. Элементы S_ij матрицы равны числу дуг, направленных из i -й вершины в j -ю.

В случае неориентированного графа ему вместе с ребром (x_i,x_j) принадлежит и ребро (x_j,x_i), поэтому матрица будет симметрической.

Пример. Для заданного ориентированного графа (рис. 12.11) построить матрицу смежности вершин:

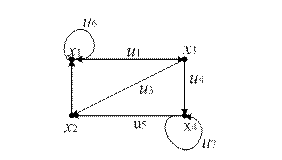
Рис 12.11

Матрица смежности вершин орграфа:

.

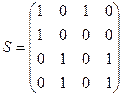Определение 12.5. Матрица смежности дуг орграфа – квадратная матрица m -го порядка (m – число дуг). Строки и столбцы матрицы соответствуют дугам графа. Элементы q_ij равны 1, если дуга u_i непосредственно предшествует дуге u_j, и нулю в остальных случаях.

Для неориентированного графа матрица смежности дуг симметрическая с элементами равными 1, если ребра имеют общую вершину, и 0 в остальных случаях.

Пример. Для заданного ориентированного графа (рис. 12.12) построить матрицу смежности дуг:

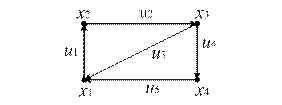
Рис.12.12

Матрица смежности дуг орграфа:

.

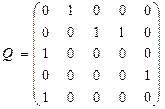Расчеты в задачах, связанных с графами, заметно упрощаются, если их элементы упорядочены.

Определение 12.6. Вершина x_i предшествует вершине x_j, если существует путь из x_i в x_j, тогда x_i называется предшествующей вершине x_j, а x_j – последующей за x_i.

Под упорядочением вершин связного орграфа без контуров понимают такое разбиение его вершин на группы, при котором:

1) вершины первой группы не имеют предшествующих, а вершины последней – последующих;

2) вершины любой другой группы не имеют предшествующих в следующей группе;

3) вершины одной и той же группы дугами не соединяются.

В результате упорядочения элементов получают граф, изоморфный данному.

Графический способ упорядочения вершин – алгоритм Фалкерсона:

1) Находят вершины графа, в которые не входит ни одна дуга. Они образуют первую группу.

2) Вершины и исходящие из них дуги исключают из дальнейшего рассмотрения (то есть вычеркивают).

3) Устанавливается следующая группа вершин, в которую не входит ни одна дуга. Этот шаг повторяют до тех пор, пока все вершины не будут упорядочены.

Пример. Упорядочить вершины орграфа (рис. 12.13):

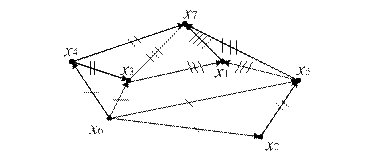
Рис. 12.13

Упорядочим вершины орграфа по алгоритму Фалкерсона (рис. 12.14):

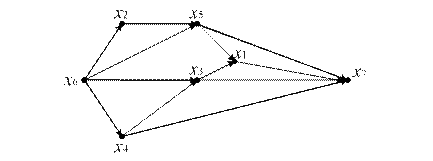
Рис. 12.14

Определение 12.7. Сеть – это взвешенный конечный орграф без циклов и петель, ориентированный в одном общем направлении от вершины I, являющейся входом (истоком) графа, к вершине S, являющейся выходом (стоком) графа.

Для наглядности будем представлять, что по дугам из истока I в сток S направляется некоторое вещество (груз, ресурс, информация и т.п.)

Определение 12.8. Максимальное количество r_ij вещества, которое может пропустить за единицу времени дуга, идущая из вершины x_i в x_j называется его пропускной способностью. В общем случае r_ij ≠ r_ji.

Определение 12.9. Количество x_ij вещества, проходящего через дугу из вершины x_i в x_j в единицу времени, называется потоком по дуге.

Предполагается, что если из вершины x_i в x_j направляется поток величиной x_ij, то величина потока из x_j в x_i равна – x_ij, то есть x_ji = –x_ij. (12.1)

Принимается также, что x_ii= 0. (12.2)

Определение 12.10. Совокупность X= { x_ij } потоков по всем дугам сети называется потоком по сети или просто потоком.

Поток по любой дуге не превышает его пропускную способность:

x_ij ≤ r_ij 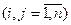. (12.3)

Если x_ij<r_ij, то дугу между вершинами x_i и x_j называют ненасыщенной.

Общее количество вещества, вытекающего из истока I, совпадает с общим количеством вещества, поступающего в сток S, то есть мощность потока 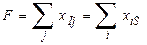(12.4),

где j – конечные вершины дуг, исходящих из I; i – начальные вершины дуг, входящих в S.

Задача о максимальном потоке формулируется следующим образом: найти совокупность X^*= { x^*_ij } потоков x^*_ij по всем дугам сети, которая удовлетворяет условиям (12.1) – (12.3) и максимизирует линейную функцию (12.4).

К задаче о максимальном потоке сводятся задачи: доставка груза; отыскание минимальной по стоимости плана выполнения комплекса работ при заданной его продолжительности; задачи, связанные с наиболее экономным строительством энергетических сетей и т.д.

Дата добавления: 2014-01-13