Разрез на сети. Теорема Форда-Фалкерсона. Алгоритм решения задачи о максимальном потоке

Пусть дана сеть (рис.12.15):

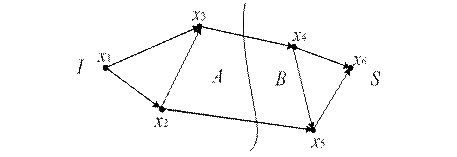
Рис. 12.15

Разобьем множество вершин этой сети на два непересекающихся подмножества А и В так, чтобы исток I попал в подмножество А, а сток S – в подмножество В.

Определение 12.11. Совокупность дуг, начальные вершины которых принадлежат подмножеству А, а конечные – подмножеству В, называют разрезом сети и обозначают А/В.

Определение 12.12. Величина , представляющая собой сумму пропускных способностей r_ij всех дуг разреза, называется пропускной способностью разреза.

Определение 12.13. Величина 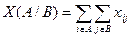, представляющая собой сумму потоков x_ij по всем дугам разреза, называется потоком через разрез.

Теорема 12.1. (Теорема Форда-Фалкерсона) На любой сети максимальная величина потока из истока I в сток S равна минимальной пропускной способности разреза, отделяющего I от S.

Алгоритм построения максимального потока:

1) Построить некоторый начальный поток X ⁰ = { x ⁰ _ij }. При этом, чем больше величина построенного потока, тем быстрее решается задача.

2) На основе заданной сети строится новая сеть:

а) любая дуга, для которой x ⁽⁰⁾ _ij= 0, остается в новой сети с первоначальной пропускной способностью r_ij;

б) любая дуга, для которой x ⁽⁰⁾ _ij ≠ 0, заменяется на две: одна дуга того же направления с пропускной способностью r_ij–x ⁽⁰⁾ _ij; вторая дуга противоположного направления с пропускной способностью x ⁽⁰⁾ _ij.

3) Если в новой сети можно найти ненулевой поток из I в S, то этот поток прибавляется к предыдущему. В результате получается новый поток X ⁽¹⁾ и переходят к пункту 2.

Если же в новой сети отсутствуют ненулевые потоки из I в S, то максимальный поток построен.

Пример. Сформировать на сети поток максимальной мощности (рис. 12.16):

Рис. 12.16

В соответствии с алгоритмом построения максимального потока сформируем на сети поток (рис. 12.17):

Рис. 12.17

Исследуем построенный поток на оптимальность (рис. 12.18):

Рис.12.18

Как видно из рисунка, невозможно сформировать на сети еще какой-нибудь поток. Следовательно, получено оптимальное решение задачи. На рисунке 12.17 представлен разрез минимальной пропускной способности, его образуют ребра 1-4; 1-3; 1-2.

Максимальная мощность потока .

Ответ: .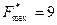

Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение выполнять оптимизационные расчеты на графовых моделях задач экономической и организационно-управленческой практики.

Тема 9. Планирование на сетях

План лекции:

1. Понятие сетевого графика (СГ)

2. Основные понятия СГ

3. Связь временных параметров СГ

4. Алгоритм расчёта параметров СГ

Дата добавления: 2014-01-13