Связь временных параметров СГ

Основные параметры СГ

Определение 13.2. Критический путь – это наиболее протяжённый по времени полный путь от истока к стоку сети. Общая продолжительность всех работ вдоль критического пути обозначается t^*.

Резерв времени R_i события i показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока наступления завершающегося события.

Полный резерв времени R_ij промежуточной работы – это максимальный запас времени, на которое можно задержать начало работы или увеличить её продолжительность при условии, что весь комплекс работ будет завершён в срок.

Свободный резерв времени r_ij промежуточной работы – это максимальный запас времени, на которое можно отсрочить или увеличить её продолжительность при условии, что не нарушатся ранние сроки начала всех последующих работ.

Замечание 13.2. Критический путь – последовательность работ и событий, не имеющих резервов времени. Общий срок завершения комплекса работ определятся продолжительностью критического пути.

Ранний срок t_j наступления события j – самый ранний момент, к которому завершаются все работы, предшествующие этому событию:

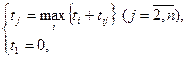(13.1)

где исток – первое событие, t_i – ранний срок наступления события i, t_ij – продолжительность работы ij.

Поздний срок T_i наступлениясобытия i – предельный момент, после которого еще остаётся ровно столько времени, сколько необходимо для выполнения всех работ, следующих за этим событием:

(13.2)

где сток – n -ое событие, T_j – самый поздний срок наступления события j.

Резерв времени R_i наступления i -того события: R_i = T_i - t_i. (13.3)

Свободный резерв времени r_ij работы ij: r_ij = t_j - t_ij - t_i. (13.4)

Полный резерв времени R_ij работы ij: R_ij = T_j - t_ij - t_i. (13.5)

4. Алгоритм расчета параметров СГ:

1) Каждое событие изобразить кружком, разделённым диаметрами на 4 сектора (рис. 13.5). В верхнем секторе записать номер события, в левом секторе, по мере вычисления, записать ранний срок t_i наступления события i, в правом – поздний срок T_i, в нижнем – резерв R_i времени события.

Рис. 13.5

2) Вычислить все ранние сроки t_i наступления событий по формулам (13.1), при этом поиск осуществляется по сетевому графику согласно номерам событий слева направо.

3) Вычислить все поздние сроки T_i наступления событий по формулам (13.2), перемещаясь по СГ от стока влево по мере убывания номеров событий.

4) Вычислить резервы времени R_i событий по формуле (13.3).

5) Выделить критический путь.

Задача. Найти критический путь и минимальное время выполнения работ сетевого графика по организации на промышленной выставке зала для демонстрации образцов продукции, выпускаемой производственным объединением (рис. 13.6).

Рис.13.6

Рассчитаем параметры сетевого графика по приведенному алгоритму, изобразив кружком, разделённым диаметрами на 4 сектора, каждое событие (рис.13.7):

Рис. 13.7

Найдем, например, свободный резерв времени r₄₆ работы 4-6:

r₄₆ = t₆ – t₄₆ – t₄ =25-1-13=11;

полный резерв времени R₃₅ работы 3-5:

R₃₅ = T₅ – t₃₅ – t₃ = 13-2-8=3.

Ответ: минимальное время выполнения работ сетевого графика .

Замечание 13.3. Резерв времени R_i события i позволяет варьировать сроки наступления события i в пределах t_i + T_i.

Замечание 13.4. Свободные резервы времени работ с учётом их значений можно использовать (отсрочить начало или затянуть окончание) по всем некритическим работам сети одновременно, не изменив t^*.

Замечание 13.5. Полные резервы времени использовать одновременно удаётся не всегда.

Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение осуществлять выбор объектов финансовых инвестиций; умение рассчитывать календарно-плановые нормативы, определять резервы времени продолжительности выполнения промежуточных заданий при регламентированном сроке завершения всего комплекса работ.

ЛИТЕРАТУРА

1. Волошин Г.Я. Методы оптимизации в экономике: Учебное пособие. – М.: Издательство «Дело и Сервис», 2004. – 320 с.

2. Высшая математика: Математическое программирование: Учеб. пособие / А.В. Кузнецов, В.А. Сакович, Н.И. Холод и др.; Под общ. ред. А.В. Кузнецова. – Мн.: Выш. шк., 1994. – 286 с.

3. Исследование операций в экономике: Учеб. пособие для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2004. – 407 с.

4. Макарова И.Л., Киселева Л.Г. Курс лекций по математике (IV семестр) для студентов-заочников экономических специальностей. – Сочи: РИО СГУТиКД, 2004. – 44 с.

5. Макарова И.Л., Якунина Н.Ф. Учебное пособие по решению задач линейного программирования. – Сочи: РИО СГУТиКД, 1997. - 25 с.

6. Общий курс высшей математики для экономистов: Учебник / Под ред. В.И. Ермакова. – М.: ИНФРА-М, 2001. – 656 с.

7. Пантелеев А.В. Методы оптимизации в примерах и задачах: Учеб. пособие / А.В. Пантелеев, Т.А. Летова. – М.: Высш. шк., 2002. – 544 с.

8. Самарин В.И. Математика: Учебно-методические материалы для студентов юридических специальностей. – Сочи: СГУТиКД, 2005. - 168 с.

9. Сборник задач и упражнений по высшей математике: Математическое программирование: Учеб. пособие / А.В. Кузнецов, В.А. Сакович, Н.И. Холод и др.; Под общ. ред. А.В. Кузнецова. – Мн.: Выш. шк., 1995. – 382 с.

10. Таха Х.А. Введение в исследование операций, 7-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2005. – 912 с.

11. Хазанова Л.Э. Математические методы в экономике: Учеб. пособие. – 3-е изд., стереотип. – М.: Волтерс Клувер, 2005. – 144 с.

12. Макарова И.Л. Учебное пособие по решению транспортной задачи. – Сочи: РИО СГУТиКД, 2000.

13. Кузнецов Ю.Н. Кузубов В.И., Волощенко А.Б. Математическое программирование: Учеб. пособие для вузов. – М.: Высшая школа, 1976. – 352 с.

14. Калихман И.Л. Сборник задач по математическому программированию. – М.: Высшая школа, 1975. – 270 с.

15. Замков О.О. Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М.: Изд-во МГУ, Изд-во «ДИС», 1997. – 368 с.

16. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. – М.: Высшая школа, 1986. – 319 с.

17. Волков И.К., Загоруйко Е.А. Исследование операций: Учебник для вузов. – М.: Изд-во МГТУ, 2000. – 436 с.

18. Аронович А.Б., Афанасьев М.Ю., Суворов Б.П. Сборник задач по исследованию операций. – М.: Изд-во МГУ, 1997. – 256 с.

Дата добавления: 2014-01-13