Частотные характеристики связанных колебательных контуров

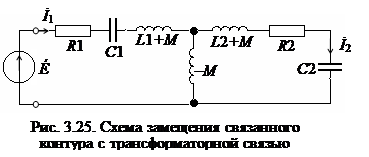Рассмотрим в качестве примера контур с трансформаторной связью. Для анализа воспользуемся схемой замещения (рис. 3. 25), в которой учтено встречное включение катушек трансформатора.

Z ₁₁ = R ₁ + j (ω L ₁ – 1/ω C ₁ ):

Z ₂₂ = R ₂ + j (ω L ₂ – 1/ω C ₂ );

Z ₁₂ = – j ω M.

Рассмотрим случай, когда параметры элементов контуров одинаковы:

R ₁ = R ₂ = R; L ₁ = L ₂ = L; C ₁ = C ₂ = C; Z ₁₁ = Z ₂₂ = R + j (ω L – 1/ω C) = R (1 + j a (ω)),

где a (ω) = Q (ω/ω₀ – ω₀/ω) – обобщенная расстройка одиночного контура;

Q = ρ/ R – добротность контура; – резонансная частота контура.

Подставив эти параметры в (3.44), найдем выражение комплексного действующего значения тока вторичного контура:

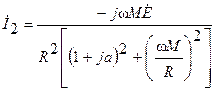. (3.45)

Можно провести ряд преобразований в выражении (3.45):

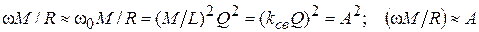, (3.46)

где k_св= M/L – коэффициент связи, определяющий степень связи между индуктивностями;

A = k_свQ – фактор связи – обобщенный параметр связи.

- комплексный ток. (3.47)

Действующее значение (модуль) тока вторичного контура равно:

. (3.48)

На резонансной частоте (a = 0) при A = 1 ток в контуре достигает максимально возможное значение

I _{2 max max} = E/ 2·R.

Запишем нормированную АЧХ тока I ₂

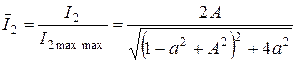. (3.49)

Анализ формулы (3.49) показывает, что форма АЧХ зависит от фактора связи A. АЧХ имеет ряд экстремальных точек, которые можно определить по экстремумам знаменателя выражения (3.49). Приравнивая первую производную знаменателя по a, получим уравнение

A(a² + 1 – A²) = 0. (3.50)

Уравнение (3.50) имеет три решения:

a ₁ = 0; .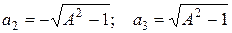

Точка a ₁= 0 является точкой максимума АЧХ, если A ≤ 1, и точкой минимума, если A > 1. В точках a _2,3, которые имеют смысл лишь при A ≥ 1, АЧХ достигает максимального значения.

При A < 1 резонансные АЧХ имеют единственный максимум при a = 0 (ω = ω₀), причем, с увеличением A резонансное (максимальное) значение тока растет (рис. 3.26, а).

При A = 1 ток достигает максимального значения. Этот случай соответствует оптимальной связи. Значение A = 1 называют критическим – A = A _кр = 1, а связь – оптимальной.

При A < 1 связь между контурами называется слабой.

При A > 1 реализуется режим сильной связи (рис. 3.26, б). Резонансные кривые становятся «двугорбыми» С ростом фактора связи A максимумы кривых все более отходят от центральной частоты, т.е. растет полоса пропускания, но увеличивается провал. Этот провал при A = 2,41 достигает относительного уровня полосы пропускания 0,707 (рис. 3.26, б). Если A > 2,41 (см. A = 4) полоса пропускания разбивается на два участка. При A = 0,67 полоса пропускания связанных контуров равна полосе пропускания одиночного контура; при A = 2,41 полоса пропускания связанных контуров в 3,1 раза превосходит полосу пропускания одиночного колебательного контура. При критической связи A_кр = 1 нормированная полоса пропускания равна ≈ 1,41.

По сравнению с формой АЧХ одиночного колебательного контура форма АЧХ связанных колебательных контуров значительно ближе к прямоугольной.

Таким образом, по сравнению с одиночными колебательными контурами связанные контуры обладают лучшими избирательными свойствами.

Дата добавления: 2014-01-13