Переходные процессы в цепи второго порядка

Рассмотрим пример подключения источника постоянного напряжения e (t) = E ₀ к последовательной RLC – цепи (рис. 4.4).

Цепь содержит два независимо включенных реактивных элемента, поэтому процессы в ней описываются ДУ второго порядка, а для определения постоянных интегрирования необходимо задать два независимых начальных условия. Если ЭДС идеального источника изменяется во времени по закону

то независимые начальные условия цепи имеют нулевые значения

u_C (0) = u_C (–0) = 0; i_L (0) = i_L (–0) = 0. (4.12)

Составим уравнение электрического равновесия цепи для контура при t ≥ 0:

. (4.13)

Подставим независимые начальные условия (4.12) в уравнение (4.13)

. (4.14)

Дифференцируя правую и левую части (4.13), получим ДУ рассматриваемой цепи после коммутации:

. (4.15)

Это уравнение линейное и однородное второго порядка, поэтому решение, т. е. ток i (t) при t ≥ 0 содержит только свободную составляющую:

. (4.16)

Характеристическое уравнение последовательной RLC -цепи

Lp ² + Rp + 1/ C = 0

имеет два корня:

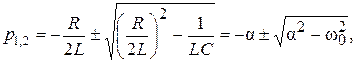(4.17)

где α = R/ 2 L – коэффициент затухания; – резонансная частота цепи.

Выражение (4.17) можно преобразовать к виду

. (4.18)

Продифференцируем правую и левую части выражения (4.16) и подставим выражение (4.14)

. (4.19)

Используя независимые начальные условия (4.12) и решая систему уравнений (4.16) и (4.19) при t ≥ 0, составим систему уравнений для определения постоянных интегрирования A ₁ и A ₂:

(4.20)

Откуда 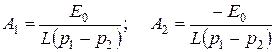. (4.21)

С учетом (4.21), (4.17) и (4.18) выражение для тока цепи после коммутации принимает вид:

. (4.22)

Выражение нормированного тока исследуемой цепи от времени имеет вид:

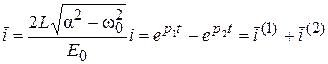. (4.23)

В зависимости от соотношения между величинами α и ω₀ (4.17), или, что тоже самое, в зависимости от величины добротности Q цепи (4.18), корни характеристического уравнения (4.17) или (4.18) могут быть вещественными различными (α > ω₀ или Q < 1/2), комплексно-сопряженными (α < ω₀ или Q > 1/2) или вещественными одинаковыми (кратными) (α = ω₀ или Q = 1/2).

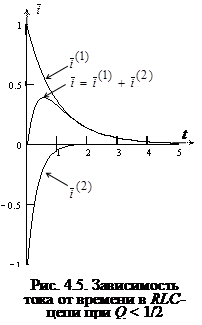
Если корни уравнения (4.17) вещественные различные (Q < 1/2), то переходный процесс носит апериодический (неколебательный) характер, причем вследствие того, что │ p ₁│<│ p ₂│, вторая составляющая нормированного тока i ⁽²⁾ затухает быстрее, чем первая i ⁽¹⁾ (рис. 4.5).

При большей добротности (Q > 1/2), корни характеристического уравнения (4.17, 4.18) будут комплексно-сопряженными

где 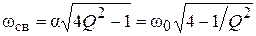– частота свободных колебаний.

Ток цепи после коммутации, как и в предыдущем случае, определяется выражением (4.16), которое после нахождения постоянных интегрирования A ₁ = E ₀/(j 2ω_св L), A ₂ = – E ₀/(j 2ω_св L) может быть преобразовано к виду

где 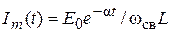– амплитуда колебаний переходного процесса.

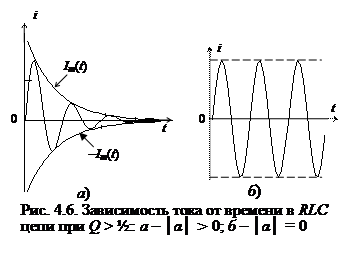Таким образом, при включении в последовательную RLC -цепь с высокой добротностью идеального источника постоянного напряжения переходные процессы в ней имеют колебательный характер (точнее, квазигармоническую функцию), амплитуда которой I_m (t) экспоненциально уменьшается во времени. Колебательный характер переходного процесса в цепи связан с периодическим обменом энергией между емкостью и индуктивностью, а затухание колебаний объясняется потерями энергии в сопротивлении. Зависимость тока цепи от времени и огибающие (амплитуда) колебания ± I_m (t) показаны на рис. 4.6, а.

Частота свободных колебаний и огибающие зависят от добротности цепи. При Q → ∞ частота свободных колебаний стремится к значению резонансной частоты ω_св → ω₀, а амплитуда колебаний не убывает, так как α → 0 (рис. 4.6, б).

При добротности Q = 1/2 корни характеристическое уравнение цепи имеет два одинаковых вещественного корня p ₁ = p ₂ = –α. Как следует из выражения (4.6), общее решение ДУ (4.2) при t ≥ 0 в этом случае имеет вид

i = i _св = (A ₁ + A ₂ t)e^{–α t} . (4.24)

Определяя с помощью независимых (4.13) и зависимых (4.14) начальных условий значения постоянных интегрирования A ₁ = 0, A ₂ = E ₀/ L и подставив их в выражение (4.24), окончательно получаем

i = E ₀ t e ^{– α t} /L.

Как и в случае вещественных различных корней, переходный процесс в цепи при одинаковых вещественных корнях имеет апериодический характер (рис. 4.7). В связи с этим, условие Q = 1/2 является предельным условием существования в цепи апериодических переходных процессов. Это режим работы цепи называется критическим.

Таким образом, характер переходных процессов в линейной RLC-цепи полностью определяется характером корней характеристического уравнения, т.е.видом цепи значениями параметров элементов.

Дата добавления: 2014-01-13