Теоремы разложения

Нахождение оригинала по изображению с помощью

Интегрирование оригинала.

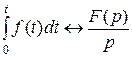. (4.29)

Операция интегрирования оригинала при преобразовании Лапласа заменяется операцией деления изображения на p.

Изображение операторной функции F (p) линейной цепи может быть представлено в виде отношения двух полиномов от p, не имеющих общих корней

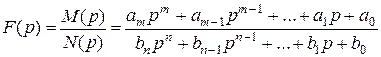, (4.30)

причем степень полинома знаменателя N (p) выше, чем степень полинома числителя M (p).

Будем считать, что полиномы M (p) и N (p) выражения (4.30) не имеют общих корней, а уравнение N (p) = 0 не имеет кратных корней.

Для нахождения оригинала f (t) разложим M (p) на простые дроби:

, (4.31)

где p_k – простые корни характеристического уравнения

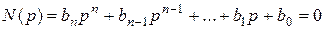, (4.32)

A_k – коэффициенты разложения.

В математике доказывается, что коэффициенты A_k можно определить по формуле

. (4.33)

Подставив значения A_k в формулу (4.31) и осуществив ряд преобразований, окончательно получим формулу оригинала по заданному изображению

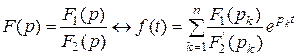. (4.34)

Формула (4.34) является математической формулировкой теоремы разложения и позволяет найти оригинал по изображению в виде (4.30), в случае простых корней.

Если среди корней p_k имеется один нулевой корень, т.е. F ₂(p) = p F ₃(p), то теорема разложения примет вид

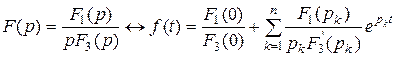. (4.35)

Если среди корней уравнения (4.32) (полюсов функции F (p)) имеются комплексно-сопряженные корни p _{k, k+1} = –α ± j ω_св, то в формуле (4.34) появится составляющая в виде затухающего гармонического колебания:

2·[ A cos(ω_св t) + B sin(ω_св t)] e ^{– α t}, (4.36)

где A и B – коэффициенты, определяемые по формуле:

. (4.37)

Дата добавления: 2014-01-13