Сетевая модель

Сетевая модель — это план или программа выполнения некоторого комплекса взаимосвязанных работ или операций, представленные в виде сетевого графика. Особенностью сете­вой модели является четкое определение всех временных вза­имосвязей предстоящих работ. Формирование такой модели связано с использованием следующих понятий:

К понятию «работа» относят:

· действительную работу, процесс, протекающий во вре­мени и не требующий затрат различных ресурсов;

· ожидание — процесс, протекающий во времени, но не требующий затрат труда;

• фиктивную работу — логическую связь между несколь­кими работами или событиями, не требующими затрат труда и материальных ресурсов. Такая работа изобра­жается на графике пунктирными линиями.

Событием называется момент завершения отдельного этапа выполнения программы или плана. Оно может быть частным результатом отдельной работы или совокупным результатом нескольких работ. Событие наступает в случае, если завер­шены все предшествующие ему работы. В сетевой модели выделяют исходные события (не имеют предшествующих ра­бот и событий) и завершающие события (не имеют последую­щих работ и событий). На сетевом графике события изобра­жаются кружками, а работы — стрелками.

Путь — это любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным со­бытием следующей за ней работы. Полный путь — это любой путь, начало которого совпадает с исходным событием сети, а конец — с завершающим. Наиболее продолжительный пол­ный путь называют критическим путем. Работы и события, находящиеся на этом пути, называются критическими.

При решении сложных задач либо комплексов задач одни и те же типовые операции могут использоваться в различ­ных комбинациях. Граф алгоритма решения задачи может быть представлен как древовидный граф, событиями (узла­ми) которого являются соответствующие операции над дан­ными, а работами — связи между отдельными операциями. На рис. 2.1 приведен граф расчета алгоритма решения задачи. В корне графа расположена начальная операция (А₀), от которой, после ее выполнения, происходит переход к опера­циям А₁ или аз, а затем - операциям А₃, А₄... А_m. Число обращений к каждой операции может быть различным.

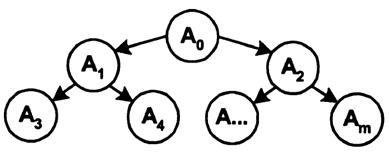
Рис. 2.1. Граф расчета алгоритма

классификация и требования к моделям

Классификация экономико-математических моделей

Экономико-математические модели классифицируют исхо­дя из особенностей моделируемого объекта, цели моделирова­ния, используемого инструментария:

· прикладные модели дают возможность оценить харак­тер функционирования объекта и сформулировать ре­комендации для принятия практических решений;

• статистические модели описывают состояние объекта (си­стемы) в конкретный момент или период времени. В таких моделях экономическая система отображается в неподвижности лишь за один период;
• динамические модели включают взаимосвязи перемен­ных во времени. В таких моделях системы рассмат­риваются в своем развитии в течение нескольких пе­риодов;
• детерминированные модели отражают теоретически предполагаемые жесткие функциональные прямые связи между переменными. В таких моделях все ограничения и целевая функция абсолютно достоверны;
• стохастические модели учитывают комплекс реальных взаимосвязей факторов и действия обратных связей. В таких моделях учитывается случайный характер про­текающих экономических процессов, для них харак­терна неопределенность.

По признаку получения точного решения модели делятся на точные и приближенные.

По специфике применяемого метода решения модели бы­вают корреляционные и регрессионные, балансовые, модели математического программирования и исследования опера­ций, модели теории графов, имитационные модели. В случа­ях, когда возможность получения оптимального решения до­казана, но необходимые для этого расчеты громоздки и тре­буют больших затрат времени, пользуются эвристическими, или экспертными методами. Эвристические методы основа­ны на накопленном опыте, интуиции. С их помощью можно получить приближенное решение поставленной задачи. При отсутствии достаточно полной информации и надежных ме­тодов составления математической модели экспертные оцен­ки являются единственным методом решения многих эконо­мических задач.

По признаку оптимальности модели подразделяются на оптимизационные, описывающие взаимодействие структурных и функциональных составляющих системы (либо поведение одной из составляющих) и неоптимизационные.

По масштабу моделируемой системы различают модели макроэкономические (межотраслевой баланс национального хозяйства), отраслевые (модели производства, распределения и потребления продукции отрасли), функциональные (модель поведения потребителей в условиях свободного рынка), моде­ли региональных комплексов.

По длительности рассматриваемого периода времени раз­личают модели краткосрочного (до 1 года), среднесрочного (до 5 лет), долгосрочного (10-15 и более лет) прогнозирования и регулирования экономики.

Требования к экономико-математическим моделям. К экономико-математическим моделям предъявляют сле­дующие требования:

· математическая модель объекта управления должна пол­но (адекватно) описывать основные закономерности его функционирования;

· модели должны быть не только эквивалентны реаль­ным проблемам, но и решаться с помощью имеющихся вычислительных средств;

· разрабатываемая модель должна быть ориентирована на использование определенных методов (или групп мето­дов), с помощью которых можно найти искомое реше­ние, причем время нахождения управляющих решений должно быть приемлемым;

· модели должны быть пригодны для непосредственного использования в процессе управления;

· модели должны быть обеспечены соответствующей ин­формацией. Как бы хорошо модель ни описывала пове­дение объекта, если на практике невозможно получить достоверные данные о значениях входящих в нее пере­менных, использовать ее невозможно;

· модели требуют наличия соответствующей нормативной базы, классификаторов, оперативно корректируемой ин­формации, адекватного технического обеспечения.

Свойства экономико-математических моделей В отношениях соответствия между системой управления и ее моделью проявляется совокупность свойств модели, кото­рые могут быть простыми и совокупными, элементными и си­стемными:

· такие свойства модели, как точность, надежность, агрегированностъ, относятся к простым элементным свойствам;

· полнота, ценность, полезность относятся к простым си­стемным свойствам;

· из простых свойств могут образовываться совокупные — семантические, синтаксические, прагматические свой­ства модели.

Наиболее объективную оценку качества модели с целью обо­снования наилучших решений можно получить с помощью оп­тимизационных методов и обобщенных показателей качества.

этапы экономико-математического моделирования

Постановка экономической проблемы и ее качественный анализ

На данном этапе формулируется сущность проблемы, при­нимаемые предпосылки и допущения, выделяются черты и свойства моделируемого объекта, изучаются его структура, взаимосвязь элементов.

Построение математической модели

Это этап формализации экономической проблемы, выраже­ния ее в виде конкретных математических зависимостей. Здесь определяется тип экономико-математической модели, изуча­ются возможности ее применения к конкретной задаче, уточ­няются перечень переменных и параметров, форма связей. Для сложных объектов обычно строится несколько моделей, каж­дая из которых характеризует лишь некоторые стороны объек­та, а другие учитываются приближенно.

Математический анализ модели

Его содержание: с помощью математических приемов ис­следования выявляются общие свойства модели и ее решений. Важным моментом является доказательство существования решения сформулированной задачи. При исследовании выяс­няется, единственно ли решение, какие переменные могут вхо­дить в решение, каковы тенденции их изменения.

Подготовка исходной информации

Это наиболее трудоемкий этап моделирования. Здесь прини­маются во внимание не только возможность получения инфор­мации требуемого качества, но и затраты на подготовку информационных массивов. При системном экономико-математичес­ком моделировании результаты функционирования одних мо­делей служат исходной информацией для других.

Численное решение

Данный этап включает разработку алгоритмов численного решения задачи, подготовку программ и непосредственное про­ведение расчетов. Численное решение существенно дополня­ет результаты аналитического исследования, а для многих задач является единственно возможным.

Анализ численных результатов и их применение

Решается вопрос о правильности и полноте результатов моделирования, применимости их как в практической дея­тельности, так и в целях усовершенствования модели. Прове­ряется адекватность модели по тем свойствам, которые были выбраны в качестве существенных.

Перечисленные этапы экономико-математического моде­лирования находятся в тесной взаимосвязи, могут иметь мес­то возвратные связи этапов.

Дата добавления: 2014-01-13