
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перестановки, размещения и сочетания
|
|
|
|
Элементы комбинаторики
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
ЛЕКЦИИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Комбинаторика – раздел математики, в котором исследуется, сколько всевозможных комбинаций (вариантов), подчиненных тем или иным условиям их образования, можно составить из элементов данного множества.
Для того, чтобы узнать количество комбинаций, обладающих определенными свойствами, можно сначала перечислить их и затем пересчитать. В большинстве случаев такой способ определения комбинаций занимает много времени, поэтому в комбинаторике, которая обслуживает теорию вероятностей, рассматривают несколько видов комбинаций: перестановки, размещения и сочетания. Эти виды комбинаций можно пересчитать по специальным формулам или с помощью основных правил комбинаторики, т.е. без непосредственного перечисления вариантов.
Правило суммы. Если элемент первого типа можно выбрать k 1 способами, элемент второго типа – k 2 способами, …, элемент s -ого типа – k s способами, то один элемент можно выбрать k 1 + k 2 + … + k s способами.
Правило произведения. Если элемент первого типа можно выбрать k 1 способами, элемент второго типа – k2 способами, …, элемент s -ого типа – k s способами, то выбрать по одному элементу каждого типа можно k 1 × k 2 × … × k s способами.
Пример 1. В мешке 6 груш, 4 яблока, 3 киви и 7 мандаринов. Сколькими способами можно выбрать один фрукт?
Решение. По правилу суммы: 6 + 4 + 3 + 7 = 20 способами.
Пример 2. На каникулы школьник получил задание: выучить доказательство любой из шести теорем, прочитать один из семи романов, написать сочинение по одной из четырех тем. Сколькими способами можно выполнить задание?
Решение. По правилу произведения: 6 × 7 × 4 = 168 способами.
Определение 1. Размещениями без повторений называют упорядоченные k-элементные подмножества n-элементного множества, содержащие различные элементы. Их количество обозначают символом  (буква А от французского слова arrangement – размещение).
(буква А от французского слова arrangement – размещение).
Определение 2. Размещениями с повторениями называют всевозможные упорядоченные k-элементные подмножества n-элементного множества. Их количество обозначают символом 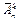 .
.
Теорема 1. Число размещений без повторений (с повторениями) вычисляется по формуле 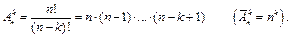
Пример 3. В непрозрачном мешке шесть фишек пронумерованных числами 1, 2, 3, 4, 5 и 6. Перемешав фишки извлекают по одной четыре и выкладывают в ряд. Получившееся число записывают, фишки возвращают в мешок и процедуру повторяют. Сколько чисел может получиться?
Решение. Элементы различные и располагаются упорядоченно (цифры четырехзначного числа), следовательно, общее число чисел равно 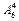 = 6!/(6 – 4)! = 6 × 5 × 4 × 3 = 360.
= 6!/(6 – 4)! = 6 × 5 × 4 × 3 = 360.
Пример 4. Последовательность четырех клеток закрашена четырьмя разными красками (одна клетка – одной краской). Сколько можно образовать четырехклеточных последовательностей, если для закрашивания можно использовать семь красок, и одной краской можно закрасить любое число клеток?
Решение. Из семи элементов образуются четырехэлементные наборы, в которых элементы могут повторяться. Обще число четырехэлементных последовательностей равно 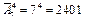 .
.
Определение 3. Перестановками из n элементов без повторений называют размещения без повторений из n элементов по n. Их количество обозначают Рn (буква Р от французского слова permutation – перестановка).
Определение 4. Перестановками с повторениями состава (k 1, k 2, …, kn) из элементов а 1, а 2, …, аn называют упорядоченные множества из k = k1 + k2 + … + kn элементов, в каждое из которых элемент а 1 входит k1 раз, элемент а 2 – k2 раз, …, элемент а n – kn раз. Их количество обозначают Р (k1, k2, …, kn).
Теорема 2. Число перестановок без повторений (с заданным числом повторений) вычисляется по формуле
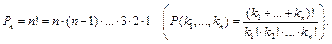
Пример 5. Сколько чисел можно получить, переставляя цифры 1, 2, 3, 4, 5, 6?
Решение. Р6 = 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720 чисел.
Пример 6. Сколько «слов» можно получить, переставляя буквы слова «галактика»?
Решение. 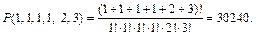
Определение 5. Сочетаниями из n элементов по k без повторений называют неупорядоченные k-элементные подмножества n-элементного множества, содержащие различные элементы. Их количество обозначают 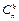 (буква С от французского слова combination – комбинация).
(буква С от французского слова combination – комбинация).
Определение 6. Сочетаниями из n-элементов по k называют всевозможные неупорядоченные k-элементные подмножества n-элементного множества. Их количество обозначают 
Теорема 3. Число сочетаний без повторений (с повторениями) вычисляется по формуле
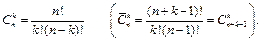

Пример 7. Сколькими способами можно составить команду из пяти человек для соревнования по плаванию, если имеются восемь пловцов?
Решение. 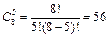 способами.
способами.
Пример 8. Сколькими способами можно разложить 20 одинаковых конфет по 5 разным мешкам?
Решение. 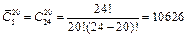 способами.
способами.
Для того, чтобы безошибочно различать виды комбинаций (перестановки, размещения и сочетания) следует применять следующие алгоритмы:
Комбинаторные задачи не всегда рассчитаны на одну формулу, а чаще всего на применение нескольких формул или правил комбинаторики.
Пример 9. В мешке 25 шаров: 4 красных, 6 синих, 7 зеленых и 8 желтых. Сколькими способами можно достать 4 шара так, чтобы среди них были хотя бы три одинаковых?
Решение. «Хотя бы три» обозначает «ровно три» или «ровно четыре». Три одинаковых шара в четверку можно выбрать 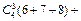

 способами, а четыре одинаковых –
способами, а четыре одинаковых – 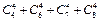 способами. Отсюда, общее число способов равно 2046 + 121 = 2167. Для решения использовалась не только формула числа сочетаний, но и основные правила комбинаторики.
способами. Отсюда, общее число способов равно 2046 + 121 = 2167. Для решения использовалась не только формула числа сочетаний, но и основные правила комбинаторики.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1783; Нарушение авторских прав?; Мы поможем в написании вашей работы!