
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Числовые характеристики случайных величин. Определение и способ задания случайной величины
|
|
|
|
Определение и способ задания случайной величины
Случайные величины
Определение 27. Случайной называют величину, которая в результате испытания примет только одно из нескольких возможных значений, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Пример 29. Число опечаток в книге – случайная величина, которая принимает целые неотрицательные значения.
Пример 30. Длина сосновой иголки – случайная величина, которая принимает значения из некоторого интервала (а, b), где а и b – положительные действительные числа.
Определение 28. Дискретной случайной величиной называют случайную величину, которая принимает отдельные, изолированные возможные значения из конечного или счетного множества (см. Пример 29).
Определение 29. Непрерывной называют случайную величину, которая может принимать все значения из некоторого интервала (конечного или бесконечного), равномощного множеству действительных чисел (см. Пример 30).
Для того, чтобы полностью задать дискретную случайную величину, достаточно перечислить все ее значения и их вероятности реализации. Такой список называют законом (рядом) распределения дискретной случайной величины, который может быть представлен таблично, графически или аналитически.
Пример 31. Составьте закон распределения дискретной случайной величины Х = {Число гербов при бросании 4 монет}.
Решение. Найдем вероятности реализации значений этой случайной величины с помощью формулы Бернулли:
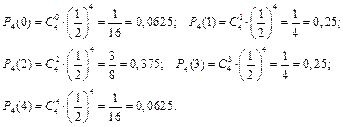
Табличное представление закона распределения
| хi | |||||
| Рi | 0,0625 | 0,25 | 0,375 | 0,25 | 0,0625 |
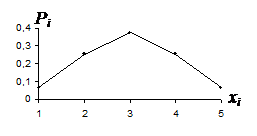 |
Рис. 2. Графическое представление закона распределения
или многоугольник распределения
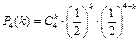 – аналитическое представление закона распределения.
– аналитическое представление закона распределения.
Замечание. Так как все значения образуют полную группу событий, то сумма их вероятностей равна единице.
Над случайными величинами как и над событиями можно выполнять действия сложения и умножения. Но эти действия выполняются с помощью законов распределения.
Определение 30. Две случайные величины Х1 и Х2 называют независимыми, если закон распределения одной не зависит от реализации тех или иных возможных значений другой величины.
Пример 32. Х1 = {Число выпавших гербов при бросании 5 монет}, Х2 = {Число очков выпавших на игральном кубике}. Эти дискретные случайные величины независимые.
Пример 33. Y1 = {Число очков, выпавших на игральном кубике}, Y2 = {Число гербов, выпавших на n монетах}, где n – значение величины Y1. Эти случайные величины зависимые, так как закон распределения Y2 зависит от реализации возможных значений Y1.
Определение 31. Суммой случайных величин Х1 и Х2 называют случайную величину Х1 + Х2, возможные значения которой образуются сложением каждого значения Х1 с каждым значением Х2, а вероятности этих возможных значений вычисляются как произведение вероятностей реализовавшихся значений слагаемых Х1 и Х2.
Пример 34. Х1 = {Число очков на I-ом кубике}, Х2 = {Число очков на II-ом кубике}.
| Х1 | ||||||
| Р1 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| Х2 | ||||||
| Р2 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Найдите закон распределения величины Х1 + Х2.
Решение. Кроме сумм 2 и 12 остальные повторяются.
| Х1 + Х2 | |||||||||||
| Р | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Сумм, дающих 2 и 12, по одной, их вероятности равны 1/6 × 1/6 и 1/6 × 1/6. Сумм, дающих 3 и 11, по две: 1 + 2, 2 + 1 и 5 + 6, 6 +5, их вероятности равны 1/6 × 1/6 + 1/6 × 1/6 и 1/6 × 1/6 + 1/6 × 1/6 как вероятности суммы несовместных событий. Сумм, дающих 4 и 10, по три: 1 + 3, 2 + 2, 3 + 1 и 4 + 6, 5 + 5, 6 + 4, их вероятности равны 1/6 × 1/6 + 1/6 × 1/6 + 1/6 × 1/6 и 1/6 × 1/6 + 1/6 × 1/6 + 1/6 × 1/6. И т.д. Получили закон распределения Х1 + Х2 = {Сумма очков на гранях двух кубиков}.
Определение 32. Произведение независимых случайных величин Y1 и Y2 называют случайную величину Y1Y2, возможные значения которой образуются умножением каждого значения Y1 на каждое значение Y2, а вероятности этих возможных значений вычисляются как произведения вероятностей реализовавшихся значений сомножителей.
Замечание. Если среди возможных значений Х1 + Х2 и Y1Y2 окажутся равные, то их вероятность следует сложить как вероятности несовместимых событий.
Для непрерывной случайной величины закон (ряд) распределения записать нельзя, так как нельзя перечислить все значения.
Для задания непрерывной случайной величины используется функция распределения F (х).
Определение 33. Функцией распределения случайной величины 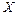 называется функция F (х) (интегральная функция распределения), значение которой равно вероятности того, что случайная величина примет значение меньше числа х: F (х) = Р (Х < х) (т.е. это вероятность выполнения неравенства Х < х).
называется функция F (х) (интегральная функция распределения), значение которой равно вероятности того, что случайная величина примет значение меньше числа х: F (х) = Р (Х < х) (т.е. это вероятность выполнения неравенства Х < х).
Свойства функции распределения:
1°. 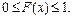
2°. Если 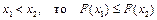 .
.
3°. Если значения непрерывной случайной величины распределены на всей числовой оси, то 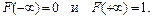
4°. Функция F (x) – непрерывная слева функция.
5°. 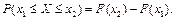
6°. Вероятность того, что непрерывная случайная величина примет значение d, равна нулю.
Пример 35. Построить функцию распределения для случайной величины примера 31. Изобразить F (х).
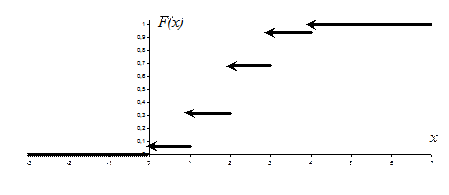 |
Решение. Пусть: 1)
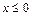 , тогда F (х) = 0 (т.к. { X < 0} – невозможное событие; 2)
, тогда F (х) = 0 (т.к. { X < 0} – невозможное событие; 2) 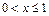 , тогда F (х) = 0,0625 (т.к. событию
, тогда F (х) = 0,0625 (т.к. событию 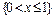 благоприятствует только { Х = 0}; 3)
благоприятствует только { Х = 0}; 3) 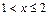 , тогда F (х) = 0,3125 (т.к. событию
, тогда F (х) = 0,3125 (т.к. событию 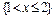 благоприятствуют два несовместимых события { Х = 0} и { Х = 1}; 4)
благоприятствуют два несовместимых события { Х = 0} и { Х = 1}; 4) 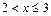 , тогда F (х) = 0,6875 (т.к. событию
, тогда F (х) = 0,6875 (т.к. событию 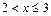 благоприятствуют три несовместимых события { Х = 0}, { Х = 1}, { Х = 2}; 5)
благоприятствуют три несовместимых события { Х = 0}, { Х = 1}, { Х = 2}; 5) 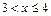 , тогда F (х) = 0,9375; 6) х >4, тогда F (х) = 1. Следовательно:
, тогда F (х) = 0,9375; 6) х >4, тогда F (х) = 1. Следовательно:
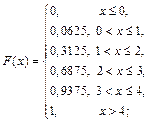
Функцию распределения F (х) можно использовать для задания дискретной случайной величины.
Непрерывную случайною величину можно также задать с помощью еще одной функции.
Определение 34. Плотностью распределения вероятностей (дифференциальной функцией распределения) непрерывной случайной величины Х называют функцию f (х), такую, что (F (х))¢ = f (х).
Свойства плотности распределения:
1°. f (х) ³ 0.
2°. 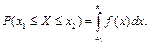
3°. 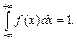
4°. 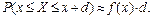
5°. 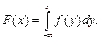
Пример 36. Непрерывная случайная величина Х задана функцией распределения 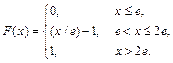
Найдите вероятность того, что Х примет значение из интервала 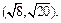
Решение. 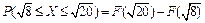 ; так как оба значения принадлежат (е, 2е], то
; так как оба значения принадлежат (е, 2е], то
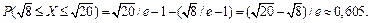
Пример 37. Найти f (х) для F (х) из примера 36.
Решение. 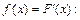 1)
1) 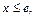 тогда
тогда 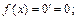 2)
2) 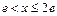 , тогда
, тогда 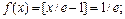 3)
3) 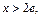 тогда
тогда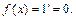 Отсюда
Отсюда
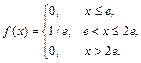
В случае, когда законы распределения случайных величин неизвестны, их сравнение осуществляется с помощью их числовых характеристик.
Определение 35. Математическим ожиданием М (Х) дискретной случайной величины Х называют сумму произведений всех возможных значений величины Х на соответствующие вероятности: 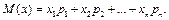
Теорема 16. Математическое ожидание дискретной случайной величины Х приближенно равно среднему арифметическому всех ее значений (при достаточно большом числе испытаний).
Определение 36. Математическим ожиданием М (Х) непрерывной случайной величины Х с плотностью вероятности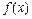 называют величину несобственного интеграла (если он сходится):
называют величину несобственного интеграла (если он сходится): 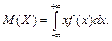
Свойства математического ожидания:
1°. Математическое ожидание постоянной равно самой постоянной величине М (С) = С.
2°. Постоянный множитель можно выносить за знак математического ожидания: 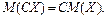
3°. Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих величин.
4°. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
Определение 37. Отклонением случайной величины Х от ее математического ожидания называется случайная величина 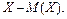
Теорема 17. Математическое ожидание отклонения 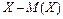 равно нулю:
равно нулю: 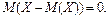
Определение 38. Дисперсией D (X) дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания: 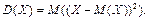
Определение 39. Дисперсией D (X) непрерывной случайной величины Х с плотностью вероятности f (x) называют величину несобственного интеграла (если он сходится): 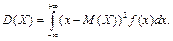
Свойства дисперсии:
1°. Дисперсия случайной величины Х равна разности между математическим ожиданием квадрата величины Х и квадратом ее математического ожидания: 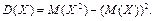
2°. Дисперсия постоянной величины равна нулю: D (С) = 0.
3°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 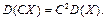
4°. Дисперсия суммы (разности) двух независимых случайных величин X и Y равна сумме их дисперсий: 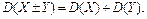
Определение 40. Средним квадратическим отклонением 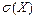 случайной величины Х называют корень квадратный из ее дисперсии:
случайной величины Х называют корень квадратный из ее дисперсии: 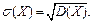
Определение 41. Начальным моментом 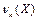 порядка k случайной величины Х называют математическое ожидание k -ой степени величины Х:
порядка k случайной величины Х называют математическое ожидание k -ой степени величины Х: 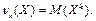
Определение 42. Центральным моментом 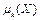 порядка k случайной величины Х называют математическое ожидание k -ой степени отклонения величины Х от ее математического ожидания:
порядка k случайной величины Х называют математическое ожидание k -ой степени отклонения величины Х от ее математического ожидания: 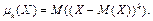
Теорема 18. Начальные и центральные моменты случайной величины Х связаны соотношениями:
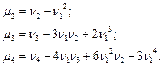
Пример 38. Найти n1, n2, n3, n4 и m1, m2, m3, m4 для: 1) дискретной случайной величины Х = {Число гербов при бросании четырех монет}; 2) непрерывной случайной величины, имеющей функцию распределения:
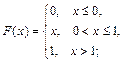
Решение. 1) Составим таблицу распределения для величины Х:
| хi | |||||
| Рi | 0,0625 | 0,25 | 0,375 | 0,25 | 0,0625 |
По определению начального момента имеем:
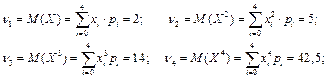
Используя утверждения последней теоремы имеем:
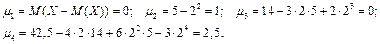
2) Найдем плотность вероятности f (х), так как числовые характеристики случайной величины определяются через f (x):
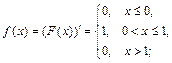
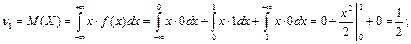
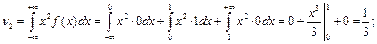
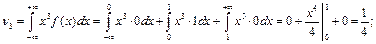
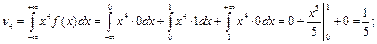
Используя утверждение последней теоремы имеем:
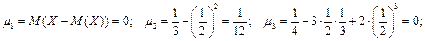
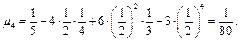
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 915; Нарушение авторских прав?; Мы поможем в написании вашей работы!