Основные виды распределения случайной величины

Наиболее часто применяемыми на практике являются следующие виды законов распределения: биномиальный, Пуассона (для дискретных случайных величин); равномерный, экспоненциальный, нормальный (для непрерывных случайных величин).

Определение 43. Биномиальным законом распределения называется закон, описывающий распределение вероятностей в схеме повторных независимых испытаний, определяемый формулой Бернулли: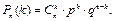

Рис. 3. Многоугольник биноминального распределения

Теорема 19. Для случайной величины Х, распределенной по биномиальному закону,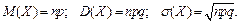

Определение 44. Распределением Пуассона называется закон, описывающий распределение вероятностей маловероятных событий (р мало) среди большого числа испытаний (n велико), причем

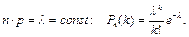
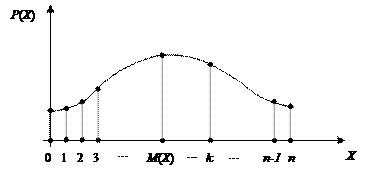Рис. 4. Многоугольник Пуассоновского распределения

Теорема 20. Для случайной величины Х, распределенной по закону Пуассона, математическое ожидание и дисперсия равны параметру l.

Определение 45. Случайная величина Х называется распределенной по равномерному закону, если ее плотность на отрезке [ a; b ] постоянна, а вне его равна нулю:

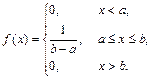
Найдем F (x) для равномерного распределения:

1) Пусть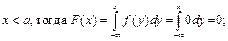

2) Пусть

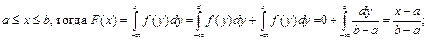
3) Пусть

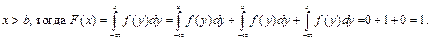
Следовательно: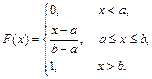

Теорема 21. Для случайной величины Х, распределенной по равномерному закону, 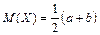и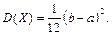

Определение 46. Случайная величина Х называется распределенной по экспоненциальному закону, если ее плотность вероятности равна

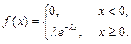
где l > 0 – параметр экспоненциального распределения.

Найдем F (x) для экспоненциального распределения:

1) Пусть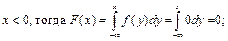

2) Пусть

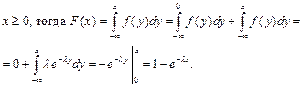
Следовательно: 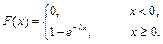Это вероятность отказа элемента за время х.

Замечание: Экспоненциальному закону подчинено время распада атомов различных элементов, а число 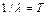носит название среднего времени распада. Кроме этого, число 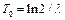называют периодом полураспада, то есть это время, в течение которого распадается половина имеющегося вещества.

Теорема 22. Для случайной величины Х, распределенной по экспоненциальному закону,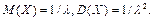

Определение 47. Случайная величина Х называется распределенной по нормальному закону, если ее плотность вероятности равна

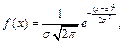где 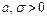– параметры нормального распределения.

Функция распределения случайной величины, распределенной по нормальному закону, имеет вид 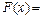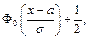где 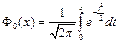– функция Лапласа, значения которой табулированы, причем 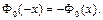(см. Приложение 3).

Теорема 23. Для случайной величины Х, распределенной по нормальному закону, М (Х) = а, D (Х) = s ².

Теорема 24. Вероятность того, что нормально распределенная случайная величина попадет в интервал [a; b], равна

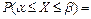
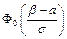
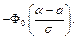
Замечание: Из последней теоремы видно, что 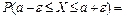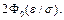В частности, если e равно трем средним квадратическим отклонениям, то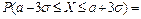 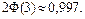Почти все значения нормальной случайной величины попадают в интервал 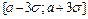почти наверняка. Этот факт называют «правилом трех сигм».

Пример 39. Все значения равномерно распределенной случайной величины лежат на интервале [1, 9]. Найти вероятность попадания случайной величины в интервал [3, 5].

Решение. По определению плотности равномерного распределения имеем 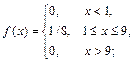тогда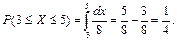

Пример 40. Книга в 1500 страниц имеет 150 опечаток. Найти вероятность того, что на случайно выбранной странице не менее четырех опечаток.

Решение. В данной ситуации случайная величина распределена по закону Пуассона: l = 150/1500 = 1/10. Имеем 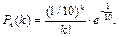Искомая вероятность и вероятность найти менее четырех опечаток в сумме дают единицу как вероятности противоположных событий. Следовательно, Р _иск.= 1 – (Р ₁₀₀₀(0) + Р ₁₀₀₀(1) + Р ₁₀₀₀(2) + Р ₁₀₀₀(3)) = 1 – (0,904837+ 0,090483 + 0,004524 + 0,000151)» 0,000004.

Пример 41. Непрерывная случайная величина распределена по экспоненциальному закону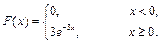

Найти вероятность попадания в интервал [0,5; 0,9].

Решение.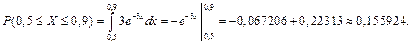

Дата добавления: 2014-01-11