Выборочный метод

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Математическая статистика – раздел математики, изучающий математические методы сбора, систематизации, обработки и интерпретации результатов наблюдений с целью выявления статистических закономерностей.

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты.

Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей выборочной совокупности, называется выборочным.

Первой задачей математической статистики следует назвать систематизацию и упорядочивание результатов наблюдений.

Пример 43.После проведения самостоятельной работы преподаватель выписал оценки, которые получили студенты: 3, 4, 5, 2, 2, 4, 3, 3, 5, 5, 4, 4, 4, 3, 4, 2, 4, 3, 3, 2, 5, 5, 3, 4, 4, 3, 2, 3, 2, 4, 3, 3, 2, 4, 2, 3, 3, 5, 3, 2, 4, 3, 3, 3, 5, 2, 2, 2, 5, 4.

Пример 44.В результате измерения некоторой величины были получены следующие числа: 12,90; 14,04; 17,50; 17,74; 18,95; 20,63; 13,33; 18,36; 17,26; 21,05; 10,94; 15,11; 12,24; 15,06; 15,16; 15,16; 12,78; 18,69; 17,50; 10,91; 19,67; 20,13; 12,16; 20,81; 19,93; 12,87; 13,94; 14,48; 11,03; 20,70; 18,84; 20,65; 13,56; 17,94; 12,03; 20,54; 11,96; 13,17; 19,74; 20,25; 20,95; 10,88; 17,77; 21,55; 15,18; 12,02; 18,82; 17,37; 11,57; 10,40.

Собранные данные прежде всего ранжируют.

Определение 48. Ряд числовых значений называют ранжированным, если все значения располагаются в порядке неубывания.

Следующим шагом в первоначальной обработке данных является их группирование, т.е. объединение результатов наблюдения в определенные сoвокупности.

Далее данные представляют в графическом виде (гистограмма или полигон), по которому выдвигаются предположения о законе распределения количественного признака) генеральной совокупности.

Сформулированные выше предположения (статистические гипотезы) проверяются с помощью специальных средств (статистических критериев). Уточняются значения параметров распределения.

Рассмотрим все эти задачи математической статистики подробнее.

Определение 49.Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.

Определение 50. Генеральной совокупностью называют совокупность объектов, из которой производится выборка.

Определение 51. Выборку называют повторной, если отобранный объект (перед отбором следующего) возвращают в генеральную совокупность. В противном случае выборку называют бесповторной.

В зависимости от конкретных условий для обеспечения репрезентативности выборки применяют различные способы отбора: простой, при котором из генеральной совокупноси извлекают по одному объекту; типический, при котором генеральную совокупность делят на части (например, по возрасту, полу, социальному положению, профессии) и отбор осуществляется из каждой части; механический, при котором отбор производится через определенный интервал (например, вопросы анкеты задаются только каждому сотому участнику); серийный, при котором объекты из генеральной совокупности отбираются группами (обследуются при помощи сплошного обследования).

Определение 52. Значения 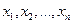, которые принимает случайная величина 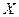в результате эксперимента (наблюдений), называются вариантами этой случайной величины.

Определение 53. Последовательность значений 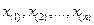случайной величины 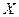, полученная в результате ранжирования, называется вариационным рядом.

Определение 54. Числа 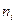, показывающие, сколько раз встречаются варианты 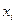в ряде наблюдений, называются частотами, а их отношение к общему числу наблюдений 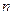(объему выборки) – относительными частотами или частостями 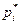, т.е. , где .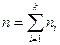

Определение 55. Числа, показывающее сколько встретилось вариантов со значением количественного признака, меньшим x, называются накопленными частотами. Отношение накопленной частоты к объему выборки называется накопленной частостью.

Определение 56. Список вариантов и их частот называется статистическим распределением выборки или статистическим рядом.

Статистическое распределение выборки является оценкой неизвестного распределения и записывается в виде таблицы, первая строка которой содержит варианты случайной величины, а вторая – их частоты.

Если случайная величина дискретна и имеет много значений признака или непрерывная, то составляют интервальный статистический ряд, который так же записывается в виде таблицы из двух строк. В первую строку записывают частичные промежутки 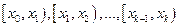, которые берут одинаковой длины 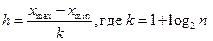- количество интервалов. За начало первого интервала следует брать величину 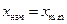. Во вторую строку записывают количество вариант, попавших в соответствующий интервал.

Рассмотрим перечисленные понятия на следующих примерах.

Пример 45. Для рассмотренных выше примеров построить вариационные ряды.

2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5.

10,40; 10,88; 10,91; 10,94; 11,03; 11,57; 11,96; 12,02; 12,03; 12,16; 12,24; 12,78; 12,87; 12,90; 13,17; 13,33; 13,56; 13,94; 14,04; 14,48; 15,06; 15,11; 15,16; 15,16; 15,18; 17,26; 17,37; 17,50; 17,50; 17,74; 17,77; 17,94; 18,36; 18,69; 18,82; 18,84; 18,95; 19,67; 19,74; 19,93; 20,13; 20,25; 20,54; 20,63; 20,65; 20,70; 20,81; 20,95; 21,05; 21,55.

Теперь построим статистические ряды:

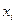
	2	3	4	5
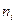
	12	17	13	8

В 43 примере количественный признак является дискретной (прерывной) случайной величиной. Сумма частот должна равняться объему выборки, т.е. 12+17+13+8=50.

Так как количественный признак во 44 примере является непрерывной величиной, то в статистическом ряду вместо вариант записывают интервалы(середины интервалов), а в качестве частот – частоты попадания значений количественного признака в данный интервал.

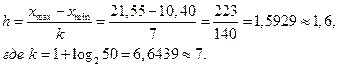
Интервал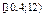
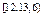
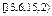
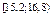
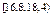
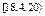
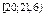
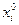
	11,2	12,8	14,4	16	17,6	19,2	20,8
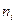
	7	10	8	0	8	7	10

Определение 57. Эмпирической (статистической) функцией распределения называется функция 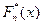, которая каждому событию 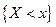ставит в соответствие его относительную частоту: .

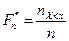При увеличении числа наблюдений относительная частота события 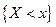приближается к его вероятности, т.е. эмпирическая функция является оценкой теоретической функции распределения 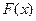случайной величины .

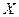Теорема 28 Пусть 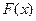- теоретическая функция распределения случайной велечины 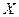и 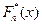- эмпирическая. Тогда для любого .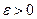

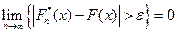Определение 58.Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами .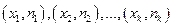

Определение 59.Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины 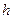, а высоты равны отношению 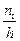- плотность частоты.

Определение 60. Кривую накопленных частот (частостей) называют кумулятой частот (частостей).

Аналогично определяются понятия гистограммы и полигона для относительных частот. Гистограмма является оценкой дифференциальной функции распределения. Кумулята является оценкой интегральной функции распределения.

Пример 46. Построить полигон частот и гистограмму для примера 45.

Изобразим декартову систему координат на плоскости. На оси Ox отложим значения вариант, а на оси Oy отложим частоты с которыми наблюдаются эти значения в выборке. Получим следующие рисунки:

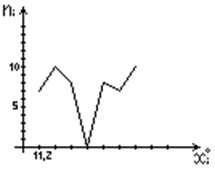
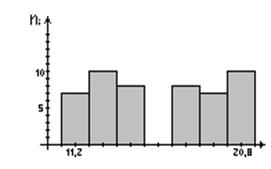
В математической статистике для значений наблюдаемого количественного признака определяются понятия числовых характеристик аналогичных характеристикам случайных величин в теории вероятностей.

Определение 61.Выборочным средним 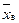называется среднее арифметическое всех значений выборк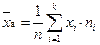и: или .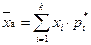

Свойства выборочного среднего:

1. Выборочное среднее константы равно самой константе.

2. Если все варианты увеличить или уменьшить в одно и то же число раз, то выборочное среднее увеличится или уменьшится во столько же раз.

3. Если все варианты увеличить или уменьшить на одно и то же число, то выборочное среднее увеличится или уменьшится на это же число.

4. Выборочное среднее отклонений ваариантов от выборочной средней вариационного ряда равна нулю.

5. Выборочное среднее алгебрайческой суммы нескольких признаков равно алгебраической сумме выборочных средних слагаемых.

Определение 62. Выборочной дисперсией 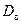называется среднее арифметическое квадратов отклонений значений выборки от выборочной средне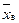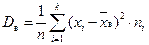й : или .

Определение 63. Выборочным средним квадратическим отклонением называется корень квадратный из выборочной дисперсии: .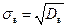

Определение 64. Исправленной выборочной дисперсией называется величина 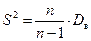, где 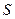- исправленное среднее квадратическое отклонение.

Замечание. При большом объеме выборк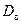и и 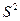мало отличаются друг от друга, поэтому исправленную дисперсию применяют для выборок малого объема ().

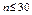Для непрерывно распределенного признака генеральной совокупности используются те же числовые характеристики, но вместо вариант используются середины интервалов.

Определение 65. Размахом вариационного ряда называется число .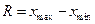

Определение 66. Модой 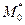вариационного ряда называется варианта, имеющая наибольшую частоту.

Определение 67. Медианой 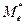вариационного ряда называется значение количественного признака, приходящееся на середину ряда. Если количество вариант четное, то в качестве медианы принимают среднее арифметическое двух вариант стоящих в центре.

Заметим, что кроме этих числовых характеристик статистического ряда принято рассматривать следующие показатели вариации.

Определение 68. Начальным моментом s–го порядка вариационного ряда называется величина .

Определение 69. Центральным моментом 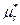s–го порядка вариационного ряда называется величина .

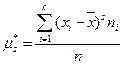Определение 70. Ассиметрией вариационного ряда называется величина .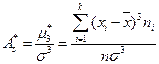

Определение 71. Эксцессом 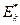вариационного ряда называется величина .

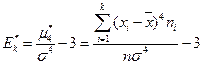Пример 47.Найти перечисленные числовые характеристики для статистических распределений примера 45.

Решение: 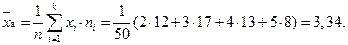Для нахождения выборочного среднего второго статистического распределения следует вместо 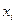взять середины интервалов:

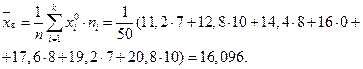
Следует отметить, что 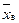вычисленное по несгруппированным данным равно 16,1244. Это отличие будет тем меньше, чем больше объем выборки.

Найдем дисперсии:

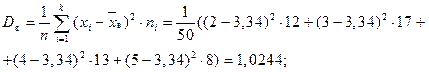
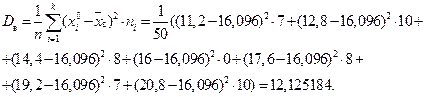
Найдем средние квадратические отклонения: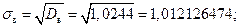

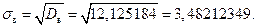
Для первого статистического распределения мода и медиана равны 3. У второго – две моды, а медиана равна (15,8+17,26)/2=16,53.

Вычислим моменты, ассиметрию и эксцесс для второго случая. По определению начального момента имеем:

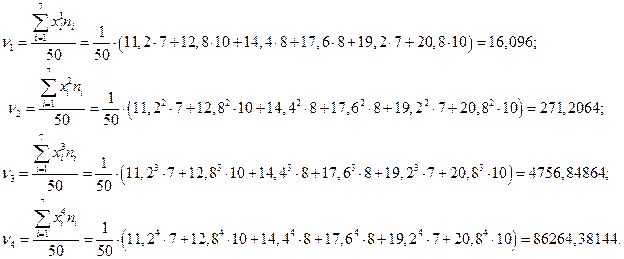
Используем известные по курсу теории вероятностей соотношения между начальными и центральными моментами:

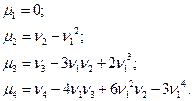
Тогда:

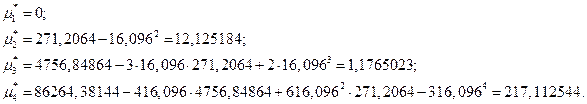
Вычислим по определениям ассиметрию и эксцесс:

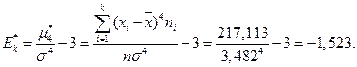
Дата добавления: 2014-01-11