Проверка статистических гипотез

Определение 77. Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известного распределения.

Определение 78. Нулевой (основной) гипотезой называют выдвинутую гипотезу .

Определение 79. Конкурирующей (альтернативной) гипотезой называют гипотезу , которая противоречит нулевой.

Определение 80. Простой называют гипотезу, содержащую только одно предположение.

Определение 81. Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

При статистической проверке гипотезы можно допустить следующие ошибки:

1. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

2. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Замечание: Вероятность совершить ошибку первого рода называют уровнем значимости и обозначают . Обычно его принимают равным 0,05 или 0,01. Если принят уровень значимости , то это значит, что примерно в одном случае из ста можно допустить ошибку первого рода. Для уменьшения возможности допустить ошибку первого рода эксперимент проводят повторно с большей выборкой.

Определение 82. Статистическим критерием называют случайную величину , по значениям которой судят о справедливости нулевой гипотезы.

Определение 83. Наблюдаемым значением называют значение статистического критерия, вычисленное по выборочным данным.

После выбора некоторого критерия проверки статистической гипотезы множество всех его возможных значений разбивают на два непересекающихся подмножества. Если наблюдаемое значение критерия попадает в первое подмножество (область принятия гипотезы), то основная гипотеза принимается. Если – во второе подмножество (критическая область), то основная отвергается и принимается альтернативная гипотеза. Точки разделяющие эти подмножества называют критическими.

Для проверки статистической гипотезы поступают следующим образом:

1. Ранжируют данные

2. Строят статистический ряд.

3. Вычисляют теоретические вероятности попадания в каждый интервал группирования по формуле: .

4. Вычисляют теоретические частоты по формуле: .

5. Задают уровень значимости .

6. Определяют критическую точку (правосторонняя критическая область) исходя из условия и количества степеней свободы (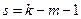, где - количество интервалов группирования признака, - количество параметров рассматриваемого распределения. Например, для нормального распределения , т.к. оно определяется двумя параметрами – математическим ожиданием и средним квадратическим отклонением).

7. Вычисляют по выборке наблюдаемое значение критерия.

8. Если наблюдаемое значение больше критического, то гипотезу отвергают; в противном случае нет оснований отвергнуть гипотезу (отвергают гипотезу более категорично, чем принимают).

В качестве критерия проверки статистических гипотез будем рассматривать критерий Пирсона 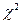(хи квадрат).

Для определения критических точек распределения 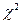при различных уровнях значимости составлены специальные таблицы.

Определение 84. Наблюдаемым значением критерия Пирсона называется величина .

Пример 48. Дана выборка, проверить гипотезу при уровне значимости , если

Решение: Объем выборки равен 100, следовательно количество интервалов группирования равно: Длина интервала группирования равна отношению размаха и количества интервалов группирования: Заметим, что значение длины интервала всегда следует округлять с избытком. В противном случае наибольшие варианты могут не включиться в последний интервал. Если же округлять с избытком на значительную долю, то последний интервал может оказаться пустым. Занесем все данные в следующую таблицу:

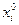
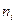
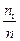
Номер интер вала	Интервал	Середина интервала	Частота	Частость	Компоненты среднего	Отклонения от среднего	Компоненты дисперсии	Теоретич. частости	Теоретич. частоты	Компоненты
	2,47 – 12,57	7,52		0,01	0,0752	-39,592	15,67526	0,0130495	1,304953	0,071264
	12,57 – 22,67	17,62		0,06	1,0572	-29,492	52,18668	0,0482933	4,829328	0,283781
	22,67 – 32,77	27,72		0,17	4,7124	-19,392	63,92844	0,1219021	12,19021	1,897759
	32,77 – 42,87	37,82		0,12	4,5384	-9,292	10,36095	0,2098788	20,98788	3,848982
	42,87 – 52,97	47,92		0,24	11,5008	0,808	0,156687	0,246467	24,64669	0,016969
	52,97 – 63,07	58,02		0,26	15,0852	10,908	30,93596	0,1974158	19,74158	1,984029
	63,07 – 73,17	68,12		0,08	5,4496	21,008	35,30688	0,1078544	10,78544	0,719364
	73,17 – 83,27	78,22		0,06	4,6932	31,108	58,06246	0,0401907	4,01908	0,976356
					47,112		266,6133			9,7985

Наблюдаемое значение критерия равно: 9,7985. Число степеней свободы равно: . По таблице, расположенной ниже, находим: 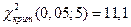. Так как наблюдаемое значение критерия меньше, чем критическое (теоретическое значение), то нет оснований отвергнуть основную (нулевую) гипотезу.

Приложение 1

Число степеней свободы
Уровень значимости
0,01	0,025	0,05
	6,6	5,0	3,8
	9,2	7,4	6,0
	11,3	9,4	7,8
	13,3	11,1	9,5
	15,1	12,8	11,1
	16,8	14,4	12,6
	18,5	16,0	14,1
	20,1	17,5	15,5
	21,7	19,0	16,9
	23,2	20,5	18,3
	24,7	21,9	19,7
	26,2	23,3	21,0
	27,7	24,7	22,4
	29,1	26,1	23,7
	30,6	27,5	25,0

Приложение 2

Таблица 2. Значение функции

х	Сотые доли х
0,0	0,39894
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
х	Десятые доли х
4,	0,0001338
5,

Приложение 3

Таблица 3. Значение функции

х	Сотые доли х
0,0	0,00000
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
х	Десятые доли х
4,	0,4999683	0,4999867	0,4999946	0,4999979	0,4999992
5,	0,4999997

Приложение 4

Таблица квантилей распределения Стьюдента .

0,95	0,99	0,999
	2,78	4,6	8,61
	2,57	4,03	6,86
	2,45	3,71	5,96
	2,37	3,5	5,41
	2,31	3,36	5,04
	2,26	3,25	4,78
	2,23	3,17	4,59
	2,2	3,11	4,44
	2,18	3,06	4,32
	2,16	3,01	4,22
	2,15	2,98	4,14
	2,13	2,95	4,07
	2,12	2,92	4,02
	2,11	2,9	3,97
	2,1	2,88	3,92
	2,093	2,861	3,883
	2,064	2,797	3,745
	2,045	2,756	3,659
	2,032	2,72	3,6
	2,023	2,708	3,558
	2,016	2,692	3,527
	2,009	2,679	3,502
	2,001	2,662	3,464
	1,996	2,649	3,439
	1,001	2,64	3,418
	1,987	2,633	3,403
	1,984	2,627	3,392
	1,98	2,617	3,374
	1,96	2,576	3,291

Приложение 5

Таблица значений .

0.95	0.99	0,999
	1,37	2,67	5,64
	1,09	2,01	3,88
	0,92	1,62	2,98
	0,8	1,38	2,42
	0,71	1,2	2,06
	0,65	1,08	1,8
	0,59	0,98	1,6
	0,55	0,9	1,45
	0,52	0,83	1,33
	0,48	0,78	1,23
	0,46	0,73	1,15
	0,44	0,7	1,07
	0,42	0,66	1,01
	0,4	0,63	0,96
	0,39	0,6	0,92
	0,37	0,58	0,88
	0,32	0,49	0,73
	0,28	0,43	0,63
	0,26	0,38	0,56
	0,24	0,35	0,5
	0,22	0,32	0,46
	0,21	0,3	0,43
	0,188	0,269	0,38
	0,174	0,245	0,34
	0,161	0,226	0,31
	0,151	0,211	0,29
	0,143	0,198	0,27
	0,115	0,16	0,211
	0,099	0,136	0,185
	0,089	0,12	0,162

Дата добавления: 2014-01-11