Понятие о выборочном наблюдении. Этапы наблюдения

Выборочное наблюдение

Выборочным называется такое не сплошное статистическое наблюдение, при котором характеристика всей совокупности дается по некоторой части, отобранной в случайном порядке.

Преимущества выборочного наблюдения заключается в существенной экономии различного вида ресурсов:

- финансовых средств, затраченных на сбор и обработку данных, подготовку кадров;

- материально-технических ресурсов;

- трудовых ресурсов, привлекаемых к обследованию;

- времени, затраченного на обработку информации.

При выборочном наблюдении обычно используют следующие показатели:

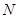- объем генеральной совокупности;

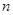- объем выборочной совокупности;

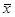- генеральная средняя, то есть среднее значение изучаемого признака по генеральной совокупности;

- Выборочное значение, то есть среднее значение изучаемого признака по выборочной совокупности;

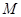- численность единиц генеральной совокупности, обладающих интересующим признаком;

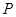- генеральная доля, то есть доля единиц, обладающих интересующим признаком в генеральной совокупности, определяется как ;

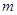- численность единиц в выборочной совокупности, обладающих интересующим признаком;

- выборочная доля, то есть доля единиц, обладающих интересующим признаком в выборочной совокупности, определяется как ;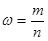

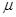- средняя ошибка выборки;

- предельная ошибка выборки.

Этапы выборочного наблюдения:

1)обоснование в соответствии с задачами исследования с целесообразностью применяемого метода;

2)составление программы проведения статистического исследования выборочным методом;

3)решение организационных вопросов сбора и обработки исходной информации;

4)установление доли выборки;

5)обоснование способов формирования выборочной совокупности;

6)осуществление отбора единиц из генеральной совокупности;

7)фиксация в отобранных единицах изучаемого признака;

8)статистическая обработка, полученной в выборке информации с определением обобщающих характеристик изучаемых признаков;

9)определение количественной оценки ошибки выборки;

10)распространение обобщенных характеристик не генеральную совокупность.

Ошибки выборочного наблюдения.

При выборочном наблюдении получаем обобщающие показатели по изучаемым варьирующим признакам. У части единиц совокупности показатель никогда не будет совпадать со свободными показателями генеральной совокупности, поэтому важно максимальное приближение показателей выборочной совокупности к показателям генеральной совокупности. В связи с этим возникает задача установления предела отклонений от этих показателей и условий, от которых зависит величина этих отклонений (установление ошибки).

Возможные пределы отклонений выборочной доли и выборочной средней от доли и средней генеральной совокупности называется ошибками выборки или ошибками репрезентативности. Ошибки выборки зависят:

- от абсолютной численности выборки;

- от степени колеблимости признака;

- от метода отбора единиц;

- от принятого уровня достоверности результатов исследования.

Указанная зависимость находит выражение в формулах средней ошибки выборки:

1. Средняя ошибка в выборочной доле

(2.1)

(повторный отбор) (бесповторный отбор)

2. Ошибка среднего значения количественного признака

(2.2)

(повторный отбор) (бесповторный отбор)

Зная среднюю ошибку выборки можно определить пределы, за которые не выйдет величина ошибочного выбора наблюдения с определенной степенью вероятности. Ошибка выборки, рассчитанная с заданной степенью вероятности, называется предельной ошибкой выборки, находится по формуле:

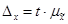, (2.3)

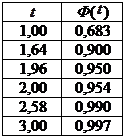где - коэффициент кратности ошибки (коэффициент доверия), его величина зависит от того, с какой вероятностью гарантируется результата выборочного обследования. Значение находят по таблице нормального закона распределения.

Исходя из предельной ошибки выборки показатели доли и средние значения признаков генеральной совокупности будут определяться:

1) при изучении доли альтернативного признака

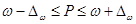(2.4)

2)при изучении средней величины количественного признака

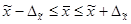(2.5)

Пример. При контрольной проверке количества поступившего товара, проведена 2 % выборка. Получили следующие данные о содержании влаги в товаре А.

% влажности	Число образцов
до 14
14-16
16-18
18-20
20 и выше
Всего

На основании данных выборочной совокупности при условии, что к нестандартной продукции относятся образцы влажности до 14 %, установите для всей совокупности с вероятностью 0,954 возможные пределы удельного веса стандартной продукции.

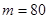
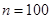
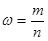
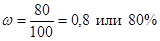
С вероятностью 0,954 можно утверждать, что доля стандартной продукции, в целом по партии товара находится в пределах от 72 до 88 %.

С вероятностью 0,997 определим возможные пределы среднего % влажности товара для всей партии

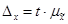
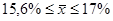
На основании проведенного выборочного обследования в вероятностью 0,997 можно заключить, что средняя влажность товара, в целом по партии товара лежит в пределах от 15,6 до 17 %.

Дата добавления: 2014-01-13