Характеристика закономерностей рядов распределения

Одной из задач анализа вариационных рядов является выявление закономерности распределения и определение ее характера. В вариационных рядах существует определенная связь в изменении частот и значении варьирующего признака. С увеличением 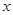величина 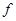сначала растет до определенной величины, а потом убывает. Такие изменения частот с изменением варьирующего признака в вариационных рядах называется закономерностями распределения. Определение это закономерности является важной задачей статистики.

В статистической практике встречаются различные распределения. Наиболее общим является распределение называемое нормальным. Закон нормального распределения предполагает:

- что отклонение от среднего значения признака является результатом большого количества мелких отклонений;

- что позитивные и негативные отклонения равновероятны;

- что наиболее вероятным значением всех в равной мере надежных измерений является их арифметическая средняя.

По нормальному закону колеблимость индивидуальных значений признака находится в пределах трех , то есть 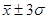. Нормальному распределению соответствует симметричное распределение. Оно описывается уравнением вида:

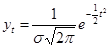, (3.1)

где 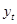- координата кривой нормального распределения;

- среднее квадратическое отклонение;

;

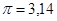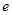- const; ;

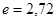- нормированное отклонение.

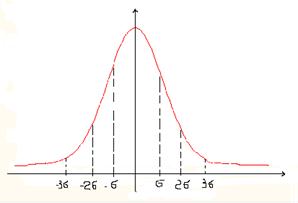
В пределах 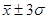при нормальном распределении находится 68,3 % всех членов распределения.

В пределах при нормальном распределении находится 95,4 % всех членов распределения.

В интервале 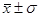- 99,7%.

Но чаще всего встречаются ассиметричные распределения. В них вершина кривой сдвинута либо вправо, либо влево и соответственно различаются правосторонняя и левосторонняя асимметрия.

левосторонняя асимметрия правосторонняя асимметрия

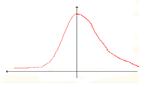
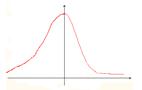
Асимметрия измеряется с помощью показателей:

1) Коэффициент асимметрии

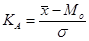, . (3.2)

Если коэффициент положителен, то наблюдается правосторонняя асимметрия, если имеет отрицательное значение – левосторонняя асимметрия.

2) Коэффициент асимметрии можно определить на основе момента третьего порядка:

, (3.3)

где 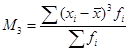- момент третьего порядка.

Оценка степени существенности этого показателя дается средней квадратической ошибки 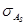, зависящий от числа наблюдений:

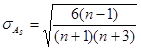. (3.4)

Если , то это говорит о не существенности асимметрии и обусловленности ее случайными факторами. Если 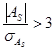, то распределение признаков совокупности не является симметричным и асимметрия признака существенна.

3) Формула Линдберга:

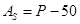, (3.5)

где 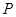- процент тех значений признака, который превосходит по величине среднюю арифметическую.

При нормальном распределении асимметрия равна нулю.

Кроме симметричности расположения кривой относительно средней арифметической, сравнение фактического распределения с нормальным производиться на определении эксцесса.

Эксцесс – островершинность, низковершинность, или плосковершинность фактической кривой распределения по сравнению с нормальным распределением.

эксцесс положителен, > 0 эксцесс <0

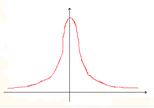
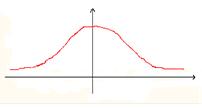
Формула Линберга эксцесса:

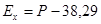(3.6)

где 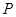- доля в % количества вариантов лежащих в интервале равном 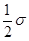в ту и другую сторону от средней арифметической в общем количестве вариант данного ряда распределения.

Расчет эксцесса может быть произведен на основе показателя центрального момента четвертого порядка:

(3.7)

где - момент четвертого порядка.

Оценка степени существенности показателя дается с помощью средней квадратической эксцесса:

. (3.8)

Если 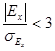, то это свидетельствует об отрицательном эксцессе и незначительной плосковершинности. Если 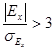, то эксцесс положителен и островершиннен.

При изучении закономерности распределения проверяется соответствие фактического распределения нормальному. Для этого подбирается и обосновывается теоретическая кривая плотности распределения достаточно точно выражающая свойственную явлению закономерность. Определяются параметры функции кривой распределения, оцениваются теоретическое и эмпирическое распределения при помощи математических критериев. Весь этот процесс называется аппроксимацией или выравниванием.

Для оценки близости эмпирического и теоретического распределения пользуются критериями согласия:

1) Критерий согласия Пирсона (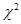) вычисляется по формуле:

, (3.9)

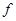где и 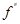- эмпирические и теоретические частоты соответственно.

Если 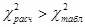, эмпирическое распределение не соответствует нормальному распределению. Если 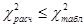, то эмпирическое распределение можно считать нормальным.

2) Критерий Ястремского (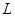) может быть найден на основе следующего отношения:

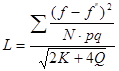, (3.10)

где 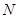- объем совокупности;

- дисперсия альтернативного признака;

- число вариантов или групп;

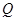- принимает значение равное 0,6 при числе вариантов или групп от 8 до 20.

Если 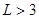, то эмпирическое распределение соответствует теоретическому.

3) Критерий Колмогорова (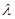) вычисляется по формуле:

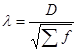, (3.11)

где 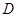- максимальное значение разности между накопленными эмпирическими и теоретическими частотами;

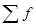- сумма эмпирических частот.

Если , то эмпирическое распределение соответствует нормальному.

Дата добавления: 2014-01-13