Дисперсия, её виды, свойства

В зависимости от образующих вариаций факторов различают виды дисперсии:

1) Общая дисперсия образуется под влиянием совокупного действия всех факторов на изучаемое явление. Рассчитывается по формуле:

. (2.1)

2) Групповая дисперсия рассчитывается, если совокупность разбита по какому-либо определенному признаку факторов. Определяется по формуле:

, (2.2)

где 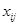- значение признака у i-той единицы j-той группы;

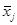- групповая средняя величина признака в j-той группе;

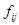- вес в j-той группе;

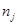- численность единиц в j-той группе.

3) Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием одного признака-фактора положенного в основу группировки. Характеризует колеблимость групповых средних около общей средней. Находится по формуле:

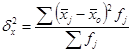. (2.3)

4) Внутригрупповая дисперсия характеризует в каждой группе вариацию, обусловленную влиянием всех прочих фактов кроме группировочного. Обобщающей характеристикой внутригрупповой дисперсии является средняя внутригрупповая дисперсия. Рассчитывается средняя внутригрупповая дисперсия по формуле:

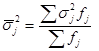. (2.4)

Существует закон, связывающий общую, межгрупповую, среднюю внутригрупповую дисперсии. Правило сложения дисперсии:

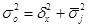. (2.5)

Зная общую дисперсию и дисперсию групповых средних можно судить о силе влияния группировочного признака в образовавшейся вариации.

Рассчитывается коэффициент детерминации (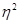), показывающий какая доля вариации, обусловлена признаком, положенным в основу группировки. Определяется он по формуле:

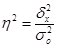. (2.6)

Корень квадратный из коэффициента детерминации представляет собой эмпирическое корреляционное отношение. Рассчитывается по формуле:

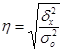. (2.7)

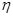изменяется от 0 до 1 (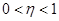). Если 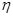=0, то группировочный признак влияет на результативный. Если 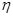=1, то группировочный признак зависит от результативного.

Свойства дисперсии:

1. Дисперсия постоянной величины равна нулю.

2. Если из всех значений вариант отнять какое-либо постоянное число 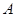, то средний квадрат отклонений не изменится:

. (2.8)

3.Если все значения вариант разделить на какое-либо постоянное число 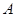, то средний квадрат отклонений уменьшится в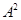раз:

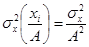. (2.9)

4. Постоянный множитель выноситься за знак дисперсии возведенный в квадрат:

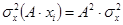. (2.10)

5. Если исчислить дисперсию от какой-либо величины 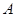, которая в той или иной степени отличается от средней арифметической, то она будет всегда больше дисперсии исчисленной от средней арифметической. При этом она будет больше на средний квадрат отклонений разности между средней и условно взятой величиной:

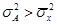
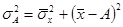. (2.11)

Использование свойств дисперсии позволяет упрощать ее расчет в случаях, когда вариационный ряд составляет арифметическую прогрессию или имеет равные интервалы.

В статистике наряду с показателями вариации количественного признака определяются показатели вариации альтернативного признака. Наличие признака обозначается через 1, отсутствие – 0. Доля вариантов обладающих интересующих признаков обозначаются буквой 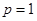, а доля вариантов, не обладающих интересующих признаков, обозначаются буквой . Таким образом, дисперсия составляет .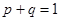

Средняя величина находится по формуле: .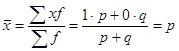

Дисперсия альтернативного признака:.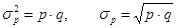

Предельное значение .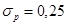

Пример. Имеются данные о реализации швейных изделий в магазине.

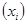
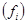
Продажа изделий за час рабочего времени, шт.	Продано товара всего, шт.	В том числе
продавцами	учениками продавцов
		-
		-
			-
			-
			-
Итого

Определить общую дисперсию, групповую дисперсию, межгрупповую дисперсию, внутригрупповую дисперсию и коэффициент детерминации.

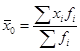
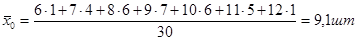
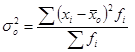
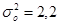
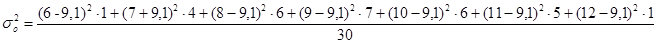
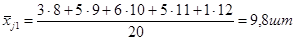
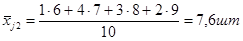
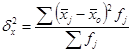
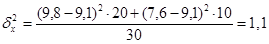
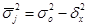
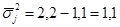
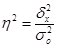
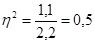
Вывод: Коэффициент детерминации 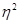показывает, что фактор квалификации работников имеет существенное значение в вариации признака, так как доля межгрупповой дисперсии составляет 5% общей дисперсии. Остальная часть вариации обусловлена влиянием других факторов.

Дата добавления: 2014-01-13