Критерий Стьюдента

Выдвигается гипотеза H₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля.

Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:

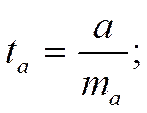
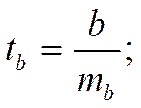
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

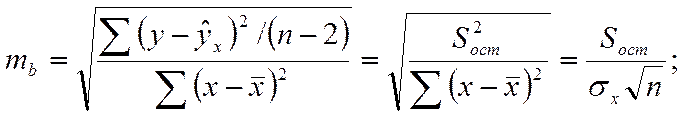
Сравнивая фактическое и критическое (табличное) значения t -статистики - t_табл и t_факт - принимаем или отвергаем гипотезу Н₀.

Если t_табл < t_факт., то H_о отклоняется, т.е. а, b и r_xy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t_табл > t_факт, то гипотеза H₀ не отклоняется и признается случайная природа формирования а, b или r _ху.

Таблица значений критерия Стьюдента (t-критерия)

Критические значения коэффициента Стьюдента (t-критерия) для различной доверительной вероятности p и числа степеней свободы f:

f	p
0.80	0.90	0.95	0.98	0.99	0.995	0.998	0.999
	3.0770	6.3130	12.7060	31.820	63.656	127.656	318.306	636.619
	1.8850	2.9200	4.3020	6.964	9.924	14.089	22.327	31.599
	1.6377	2.35340	3.182	4.540	5.840	7.458	10.214	12.924
	1.5332	2.13180	2.776	3.746	4.604	5.597	7.173	8.610
	1.4759	2.01500	2.570	3.649	4.0321	4.773	5.893	6.863
	1.4390	1.943	2.4460	3.1420	3.7070	4.316	5.2070	5.958
	1.4149	1.8946	2.3646	2.998	3.4995	4.2293	4.785	5.4079
	1.3968	1.8596	2.3060	2.8965	3.3554	3.832	4.5008	5.0413
	1.3830	1.8331	2.2622	2.8214	3.2498	3.6897	4.2968	4.780
	1.3720	1.8125	2.2281	2.7638	3.1693	3.5814	4.1437	4.5869
	1.363	1.795	2.201	2.718	3.105	3.496	4.024	4.437
	1.3562	1.7823	2.1788	2.6810	3.0845	3.4284	3.929	4.178
	1.3502	1.7709	2.1604	2.6503	3.1123	3.3725	3.852	4.220
	1.3450	1.7613	2.1448	2.6245	2.976	3.3257	3.787	4.140
	1.3406	1.7530	2.1314	2.6025	2.9467	3.2860	3.732	4.072
	1.3360	1.7450	2.1190	2.5830	2.9200	3.2520	3.6860	4.0150
	1.3334	1.7396	2.1098	2.5668	2.8982	3.2224	3.6458	3.965
	1.3304	1.7341	2.1009	2.5514	2.8784	3.1966	3.6105	3.9216
	1.3277	1.7291	2.0930	2.5395	2.8609	3.1737	3.5794	3.8834

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n - m - 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Условия использования коэффициента Стьюдента:

• Исследуемые данные подчиняются нормальному закону распределения
• Равенство дисперсий (при сравнении двух выборок)

доверительные интервалы:

,

.

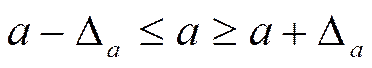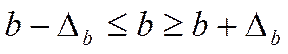предельная ошибка для каждого показателя:

.

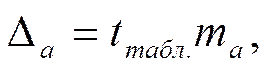
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемыйпараметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

Прогнозное значение у_р определяется путем подстановки в уравнение регрессии у_х = а + bх соответствующего (прогнозного) значения х_р.

Дата добавления: 2014-01-13