
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение 5
|
|
|
|
Определение 4
Точкой отсчета называется геометрическая точка, фиксированная в пространстве, относительно которой рассматриваются положения всех других точек пространства или какого-либо множества точек из этого пространства.
Системой отсчета называется фиксированная декартовая прямоугольная система координат (ДПСК) с началом в точке отсчета 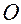 .
.
Систему отсчета будем обозначать 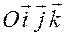 или
или 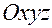 , где
, где
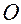 — точка отсчета, или иначе, полюс декартовой прямоугольной системы координат;
— точка отсчета, или иначе, полюс декартовой прямоугольной системы координат;
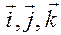 — базис ДПСК (единичные взаимно-ортогональные векторы);
— базис ДПСК (единичные взаимно-ортогональные векторы);
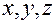 — координатные оси системы отсчета.
— координатные оси системы отсчета.


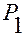
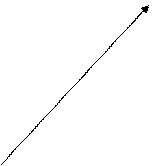
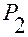
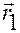
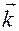
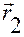


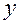


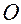
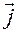
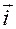
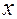
Рис. В.2.3
На рис.В.2.3 в качестве примера изображена система отсчета 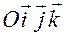 , и в ней — положения
, и в ней — положения 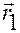 и
и 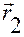 точек
точек 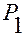 и
и 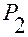 .
.
Иногда вместо ДПСК в качестве системы отсчета бывает удобнее использовать аффинную систему координат (см. рис.В.2.4).
В таких случаях этот выбор оговаривается особо. Однако при любом выборе аффинной системы ее начало совпадает с заданной точкой отсчета 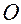 . При этом указывается базис
. При этом указывается базис 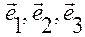 вместе с матрицей метрических коэффициентов
вместе с матрицей метрических коэффициентов  размерности
размерности 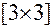 .
.

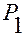

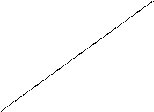
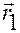
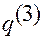
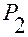

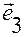
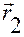




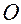
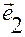
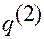
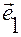
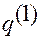
Рис. В.2.4
На рис.В.2.4 изображена система отсчета 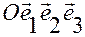 , и в ней — положения
, и в ней — положения 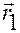 и
и 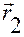 точек
точек 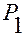 и
и 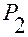 ;
;
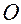 — точка отсчета (полюсаффинной системы координат
— точка отсчета (полюсаффинной системы координат 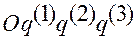 );
); 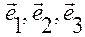 — базис аффинной системы координат (базис системы отсчета);
— базис аффинной системы координат (базис системы отсчета); 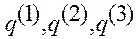 — ее координатные оси.
— ее координатные оси.
Матрица метрических коэффициентов  — симметричная. Ее элементы
— симметричная. Ее элементы 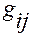 ,
, 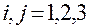 , называются метрическими коэффициентами.
, называются метрическими коэффициентами.
Они связаны с базисными векторами 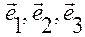 соотношениями
соотношениями
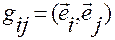 ,
, 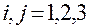 . (В.2.1)
. (В.2.1)
Из (В.2.1) легко устанавливается геометрический смысл метрических коэффициентов.
Действительно, исходя из понятия скалярного произведения векторов, можем (В.2.1) переписать в виде
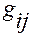
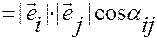 ,
,
где 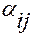 — угол между векторами
— угол между векторами 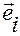 и
и 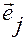 , а
, а 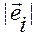 и
и 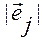 — их длины. Следовательно,
— их длины. Следовательно,
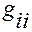
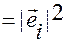 ,
, 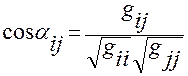 .
.
Отсюда заключаем, что
диагональные элементы метрической матрицы задают квадраты длин базисных векторов, а по остальным элементам определяются углы между базисными векторами.
В частности, если все базисные векторы — единичные (по диагонали матрицы  стоят единицы), то такая аффинная система координат называется косоугольной.
стоят единицы), то такая аффинная система координат называется косоугольной.
§3. Математические модели материальных
объектов
В основе теории механических движений в классической механике лежат следующие математические модели реальных материальных объектов:
– материальная точка;
– система материальных точек, или иначе, «механическая система»;
– неизменяемые механические системы и абсолютно твердые тела;
– деформируемые тела, жидкие и газообразные среды.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 349; Нарушение авторских прав?; Мы поможем в написании вашей работы!