Случайный процесс со счетным множеством состояний

Случайный процесс, протекающий в системе массового обслужива­ния, состоит в том, что система в случайные моменты времени пере­ходит из одного состояния в другое: меняется число занятых каналов, число заявок, стоящих в очереди, и т. п. Такой процесс существенно отличается от случайных процессов, которые мы рассматривали в гла­вах 15—17. Дело в том, что система массового обслуживания пред­ставляет собой физическую систему дискретного типа с конеч­ным (или счетным) множеством состояний ¹), а переход системы из одного состояния в другое происходит скачком, в момент, когда осу­ществляется какое-то событие (приход новой заявки, освобождение канала, уход заявки из очереди и т. п.).

Рассмотрим физическую систему X со счетным множеством состояний

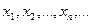
В любой момент времени t система X может быть в одном из этих состояний. Обозначим p_k(t) (k = 1, 2,..., n,...) вероятность того, что в момент t система будет находиться в состоянии x_k. Очевидно, для любого t

Совокупность вероятностей p_k(t) для каждого момента времени t ха­рактеризует данное сечение случайного процесса, протекающего в си­стеме. Эта совокупность не является исчерпывающей характеристикой процесса (она, например, совсем не отражает зависимости между се­чениями), но все же достаточно хорошо описывает процесс и для ряда практических применений оказывается достаточной.

Случайные процессы со счетным множеством состояний бывают двух типов: с дискретным или непрерывным временем. Первые отлича­ются тем, что переходы из состояния в состояние могут происходить только в строго определенные, разделенные конечными интервала­ми моменты времени t₁, t₂,… Случайные процессы с непрерывным временем отличаются тем, что переход системы из состояния в со­стояние возможен в любой момент времени t.

В качестве примера дискретной системы X, в которой протекает случайный процесс с непрерывным временем, рассмотрим группу из n самолетов, совершающих налет на территорию противника, обороняе­мую истребительной авиацией. Ни момент обнаружения группы, ни моменты подъема по ней истребителей заранее не известны. Различ­ные состояния системы соответствуют различному числу пораженных самолетов в составе группы:

х₀ — не поражено ни одного самолета,

х₁ —поражен ровно один самолет,

…..

x_k — поражено ровно k самолетов,

…..

х_n —поражены все п самолетов.

Схема возможных состояний системы и возможных переходов из состояния в состояние показана на рис. 4.1.

Стрелками показаны возможные переходы системы из состояния в состояние. Закругленная стрелка, направленная из состояния x_k в него же, означает, что система может не только перейти в соседнее

Рис. 4.1.

состояние x_k+1 но и остаться в прежнем. Для данной системы характерны необратимые переходы (пораженные самолеты не восстанавливаются); в связи с этим из состояния х_п никакие пере­ходы в другие состояния уже невозможны.

Отметим, что на схеме возможных переходов (рис. 4.1) пока­заны только переходы из состояния в соседнее состояние и не пока­заны «перескоки» через состояние: эти перескоки отброшены как практически невозможные. Действительно, для того чтобы система «перескочила» через состояние, нужно, чтобы строго одновременно были поражены два или более самолета, а вероятность такого собы­тия равна нулю.

Случайные процессы, протекающие в системах массового обслужи­вания, как правило, представляют собой процессы с непрерывным временем. Это связано со случайностью потока заявок. В противопо­ложность системе с необратимыми переходами, рассмотренной в пре­дыдущем примере, для системы массового обслуживания характерны обратимые переходы: занятый канал может освободиться, оче­редь может «рассосаться».

В качестве примера рассмотрим одноканальную систему массового обслуживания (например, одну телефонную линию), в которой заявка, заставшая канал занятым, не становится в очередь, а покидает си­стему (получает «отказ»). Это – дискретная система с непрерывным временем и двумя возможными состояниями:

х₀ — канал свободен,

х₁ — канал занят.

Переходы из состояния в состояние обратимы. Схема возможных переходов показана на рис. 4.2.

Рис. 4.2.

Рис. 4.3.

Для n-канальной системы такого же типа схема возможных пере­ходов показана на рис. 19.2.3. Состояние х₀ — все каналы свободны; х₁ —занят ровно один канал, х₂— занято ровно два канала и т. д. Рассмотрим еще один пример дискретной системы с непрерывным временем: одноканальную систему массового обслуживания, которая может находиться в четырех состояниях:

х₀ —канал исправен и свободен,

x₁ —канал исправен и занят,

х₂ —канал неисправен и ждет ремонта,

х₃ —канал неисправен и ремонтируется.

Схема возможных переходов для этого случая показана на рис. 19.2.4). Переход системы из х₃ непосредственно в х₁, минуя х₀, можно счи­тать практически невозможным, так как для этого нужно, чтобы окончание ремонта и приход оче­редной заявки произошли строго в один и тот же момент времени.

Рис. 4.4.

Для того чтобы описать случайный процесс, протекающий в дискретной системе с непрерывным временем, прежде всего нужно проанализировать причины, вызывающие переход системы из состоя­ния в состояние. Для системы массового обслужи­вания основным фактором, обусловливающим протекающие в ней про­цессы, является поток заявок. Поэтому математическое описание любой системы массового обслуживания начинается с описания потока заявок.

Дата добавления: 2014-01-13