Тема 21 Квантовомеханическое описание электронных состояний двухатомных молекул

1 Виды движения молекулы

2 Электронное движение молекулы и химическая связь

3 Квантовомеханическое описание электронного строения молекулы водорода в нулевом приближении

4 Квантовомеханическое описание электронного строения молекулы

водорода в первом приближении

5 Характеристика химической связи в молекуле водорода

Молекула – это наименьшая устойчивая частица данного вещества, обладающая основными свойствами самого вещества и состоящая из одинаковых или различных атомов, соединенных в одно целое посредством химической связи. Химические связи (химические силы) в молекуле обусловлены различными взаимодействиями внешних электронов составляющих ее атомов. Молекула совершает сложное движение, которое в системе центра масс молекулы можно представить как совокупность электронного, колебательного и вращательного движений с учетом их взаимного влияния.

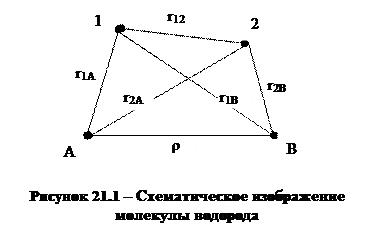
Электронное движение молекулы – это движение электронов, входящих в состав молекулы, относительно ее ядер. Энергия , соответствующая этому движению, называется электронной энергией.

Колебательное движение молекулы – это периодическое изменение взаимного расположения ядер. Энергия 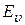, соответствующая этому движению, называется колебательной энергией.

Вращательное движение молекулы – это периодическое изменение положения молекулы как целого в пространстве. Энергия , соответствующая этому движению, называется вращательной энергией.

При рассмотрении молекул важнейшим вопросом является вопрос о природе сил, посредством которых из электрически нейтральных атомов образуется молекула, то есть вопрос о природе химической связи. В соответствии с традиционной классификацией предельными вариантами (типами) химической связи являются:

а) ионная (гетерополярная) связь,

б) ковалентная связь.

Способность атома образовывать химические связи с другими атомами или группами атомов называют валентностью. Различают два основных типа валентности, названия которых коррелируют с названиями типов химической связи: ковалентность и ионную валентность.

Ковалентность равна числу валентных связей, образованных атомом в молекуле.

Ковалентная (гомеополярная) связь характерна для атомных молекул, в которых основное состояние соответствует нормальным состояниям нейтральных атомов. Связь этого типа в ряде случаев реализуется между одинаковыми атомами (например, в молекуле водорода H_2).

Силы, обеспечивающие устойчивость атомных молекул, являются обменными и имеют специфический квантовый характер. Они действуют между внешними электронами атомов в молекуле.

Ионная валентность (гетеро- или электровалентность) равна числу электронов, отданных или полученных атомом при образовании ионной молекулы.

Ионные молекулы состоят из ионов химических элементов, входящих в молекулу. Общая сумма положительных и отрицательных зарядов ионов в молекуле равна нулю, вследствие чего ионные молекулы электрически нейтральны. Типичными ионными молекулами являются молекулы щелочно-галоидных солей, образованных ионами элементов I и VII группы Периодической системы элементов: NaCl, RbBr, CsJ и др.

Силы, обеспечивающие устойчивость ионной молекулы, в основном имеют электрическую природу.

Иногда пользуются также понятиями валентности по отношению к водороду или кислороду, определяемыми как число присоединяемых или замещаемых в молекуле атомов соответственно водорода или кислорода.

Последовательное описание всех видов химической связи возможно в рамках квантовой механики. Решая квантово-механическую задачу для электронного движения молекулы, можно описать природу химической связи в молекуле. Электронное движение молекулы рассматривается в рамках приближения Борна-Оппенгеймера как частного случая адиабатического приближения [1], суть которого состоит в пренебрежении взаимным влиянием движений различного вида, совершаемых молекулой.

На примере молекулы водорода, являющейся простейшей молекулой, в которой химическая связь осуществляется двумя электронами, познакомимся с методикой квантово-механического определения её электронных состояний. Анализируя решение этой задачи, обсудим свойства химической связи в молекулах.

Схематически строение молекулы водорода, состоящей из двух ядер, обозначенных буквами А и В, и двух электронов, обозначенных 1 и 2, показано на рисунке 21.1. На рисунке обозначены также расстояния между ядрами (ρ), электроном и ядром (r_1А, r_1В, r_2А, r_2В) и между электронами (r₁₂).

В отсутствие спин-орбитального взаимодействия функция состояния 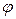электронного движения молекулы определяется произведением функции состояния орбитального движения 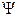и функции состояния спинового движения :

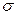. (21.1)

Функция , зависящая от пространственных координат обоих электронов, является решением уравнения Шрёдингера.

Оператор Гамильтона для для электронной оболочки молекулы водорода запишется в виде:

(21.2)

где

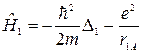(21.3)

– оператор Гамильтона первого электрона в поле ядра А,

(21.4)

– оператор Гамильтона второго электрона в поле ядра В,

(21.5)

– оператор энергии межатомного взаимодействия.

Уравнение Шредингера имеет вид:

. (21.6)

Функция состояния является функцией пространственных координат обоих электронов и зависит от межъядерного расстояния 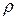молекулы как от параметра.

Данная задача не имеет точного решения, поэтому собственные функции и собственные значения оператора Гамильтона находят методом последовательных приближений.

Рассмотрим нулевое приближение, в рамках которого взаимодействие между отдельными атомами водорода отсутствует, т.е. ρ→ ∞, r_1В → ∞, r_2А → ∞, r₁₂ → ∞; при этом электрон 1 движется в поле ядра А, электрон 2 – в поле ядра В. Тогда гамильтониан рассматриваемой системы упрощается и имеет вид:

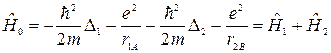. (21.7)

Уравнение (21.6) с гамильтонианом в виде (21.7) принимает вид:

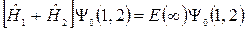. (21.8)

В этом уравнении возможно разделение переменных первого (1) и второго (2) электронов. Поэтому решение уравнения (21.8) представим в виде:

, (21.9)

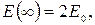(21.10)

где E₀ – полная энергия электрона 1 в поле ядра А и полная энергия электрона 2 в поле ядра В.

После учёта выражений (21.9) и (21.10) в (21.8) и выполнения разделения переменных получим два одноэлектронных уравнения:

, (21.11)

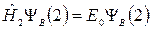. (21.12)

Если электрон 2 находится у ядра А, а электрон 1 – у ядра В, то вследствие тождественности электронов 1 и 2 получим решение, аналогичное (21.9):

.

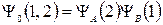Условиям симметрии относительно перестановки электронов удовлетворяют симметричная 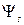и антисимметричная функции, зависящие от пространственных координат электронов:

,

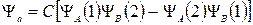, (21.13)

где С – постоянный множитель.

Полученные функции являются собственными функциями гамильтониана при описании электронного движения молекулы водорода в нулевом приближении. Если обоим электронам соответствуют одинаковые атомные орбитали, то энергия рассматриваемой системы (молекулы водорода) в нулевом приближении определяется как удвоенная полная энергия электрона в поле ядра, характерная для уединенного атома:

. (21.14)

Применяя теорию возмущений, в первом её приближении энергию молекулы находят в результате квантово-механического усреднения собственных значений оператора Гамильтона (1) по функциям нулевого приближения:

, (21.15)

где – элементарный объем, выражаемый через дифференциалы пространственных координат первого и второго электронов; , .

Выражение для постоянной 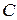определяется из условия нормировки функций состояния, представленных в виде (21.13), с учетом ортонормированности одноэлектронных функций состояния:

, (21.16)

где – интеграл перекрывания.

Воспользовавшись далее выражениями (21.2), (21.15) и (21.16) и учитывая уравнения (21.11), (21.12), для энергии электронного движения молекулы водорода в первом приближении получим:

. (21.17)

Здесь

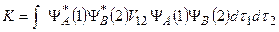> 0

– кулоновский интеграл; его значение равно среднему значению энергии электростатического взаимодействия электронов и положительно;

< 0

– обменный интеграл, характеризующий степень перекрывания одноэлектронных функций, относящихся к различным ядрам молекулы и имеющий отрицательное значение.

Запишем отдельно выражения для электронной энергии молекулы в симметричном (s) и антисимметричном (а) состоянии в первом приближении:

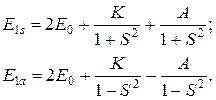(21.18)

Проиллюстрируем полученный при расчете электронной энергии результат. Предварительно введем обозначения:

; .

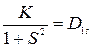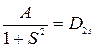
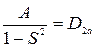Тогда выражения (21.18) можно представить в виде

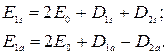(21.19)

Так как 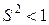, (поэтому), А < 0 (поэтому D_2s < 0, D_2a < 0), взаимное расположение энергетических уровней может быть отражено так, как это показано на рисунке 21.2.

Анализируя формулы (21.19) и схему уровней (рисунок 21.2) видим, что , следовательно, – энергия молекулы водорода в основном электронном состоянии, 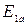– ее энергия в первом возбужденном состоянии.

Зависимость энергии молекулы в этих состояниях от межъядерного расстояния показана на рисунке 21.3.

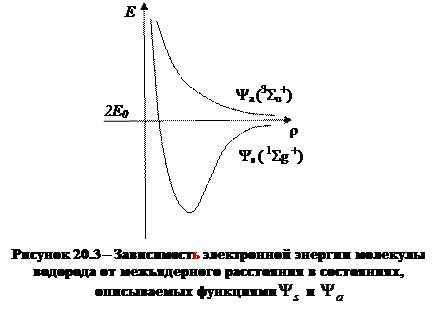На зависимости энергии молекулы от межъядерного расстояния, соответствующей состоянию, описываемому функцией , имеется область отрицательных значений энергии; соответствующие ее границам значения межъядерного расстояния ограничивают область притяжения атомов. Межъядерное расстояние, при котором функция имеет минимум, называют равновесным расстоянием. Электронное состояние, которому соответствует функция и описанная энергетическая кривая, является устойчивым.

График зависимости энергии от межъядерного расстояния, соответствующие состоянию с волновой функцией 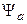, полностью локализован в области положительных значений энергии и соответствует отталкиванию атомов водорода. Состояние молекулы водорода, которому соответствует функция состояния 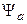, является неустойчивым.

Так как функция состояния 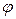(21.1) должна быть антисимметрична, основному состоянию молекулы соответствует функция

. (21.20)

Спиновая функция соответствует состоянию молекулы, в которой электроны имеют антипараллельные спины. При этом суммарное спиновое квантовое число S = 0, мультиплетность состояния æ = 2S+1=1, и соответствующее состояние молекулы является синглетным.

Первому возбужденному электронному состоянию соответствует функция

. (21.21)

Спиновая функция 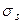соответствует состоянию молекулы, в котором суммарное спиновое квантовое число S =1 (спины электронов параллельны друг другу). При этом мультиплетность состояния æ = 2S+1=3, и состояние является триплетным.

Электронные термы молекул не отличаются по своему происхождению от электронных термов изолированных атомов. Число электронных термов значительно превышает число этих термов в атомах. Любой атом в молекуле находится в электрическом поле остальных ее атомов (внутримолекулярное электрическое поле), которое обусловливает расщепление электронных уровней, аналогичное тому расщеплению, которое характерно для атомов, находящихся в электрическом поле.

Энергетические электронные уровни молекулы определяются ее конфигурацией, то есть совокупностью квантовых чисел, соответствующих состояниям всех электронов молекулы. Систематика электронных уровней и спектров молекул основана на векторной модели молекулы, являющейся обобщением векторной модели атома.

Электрическое поле двух или большего числа атомных ядер, входящих в состав молекулы, не обладает центральной симметрией. Поэтому полный момент импульса электронов в молекуле не сохраняется. Однако для двухатомных, а также прямолинейных многоатомных молекул это поле симметрично относительно оси молекулы ОZ, проходящей через ядра атомов. В такой ситуации, пренебрегая слабым спин-орбитальным взаимодействием, можно считать, что сохраняются:

а) проекция на ось OZ суммарного орбитального момента импульса всех электронов молекулы, абсолютная величина которой, выраженная в единицах ћ, равна орбитальному квантовому числу молекулы Λ, принимающему значения 0, 1, 2, …;

б) суммарный спин всех электронов молекулы, характеризуемый квантовым числом S, которое, как и для атомных спектров, определяет мультиплетность электронного терма молекулы, равную .

В большинстве случаев классификацию электронных термов двухатомных молекул проводят по значению квантового числа Λ, подобно тому, как это делается при классификации атомных спектров по орбитальному квантовому числу L. Принято следующее обозначение электронных термов молекулы: 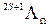, где, в зависимости от числового значения Λ = 0, 1, 2, …, используют прописные буквы греческого алфавита, ∑, Π, Δ, Φ, …, обозначающим термы, аналогичные атомным термам S, P, D, F, …

Квантовое число

Ω = Λ + ∑,

где квантовое число ∑ характеризует проекцию спина молекулы на ее ось и пробегает (2S + 1) значений: S, S – 1, …, -S (не путать число ∑ с ∑-состоянием молекулы при Λ = 0).

Симметрия двухатомной молекулы допускает не только поворот вокруг оси OZ молекулы, но и отражение в плоскости, проходящей через эту ось (например, в плоскости YOZ, то есть замену координат x_i на –x_i). При этом энергия молекулы не изменяется, а новое состояние не тождественно исходному, так как изменяется знак проекции орбитального момента импульса молекулы на ось OZ. Поэтому все состояния молекулы с Λ ≠ 0 двукратно вырождены.

Если Λ = 0 (∑-терм), при отражении в плоскости YOZ состояние молекулы не изменяется, так что ∑-терм не вырожден. При отражении волновая функция ∑-терма может только умножаться на +1 или на -1 (в результате двух последовательных отражений волновая функция не меняется).

Двухатомная молекула с одинаковыми атомными ядрами обладает центром симметрии, лежащим между ядрами. Если этот центр принять за начало координат, то при изменении знака координат всех электронов и сохранении координат ядер энергия системы не изменяется, а у волновой функции знак или изменяется (нечетная функция), или не изменяется (четная функция). Соответственно электронные термы делят на нечетные (u -термы) и четные (g-термы). Четность терма обозначается нижним индексом u или g – на месте символа Ω в спектроскопической записи терма. Для подавляющего большинства двухатомных молекул основным термом является терм , а для молекулы, состоящей из одинаковых атомов, – терм .

Запишем обозначения состояний, полученных для молекулы водорода, пользуясь спектроскопической классификацией.

Так как атомы водорода, образующие молекулу, находятся в основном состоянии, их орбитальные квантовые числа одинаковы: L₁ = L₂ = 0. Следовательно, орбитальное квантовое число молекулы в обоих электронных состояниях равно нулю (L = 0). При этом орбитальное квантовое число проекции орбитального момента импульса молекулы 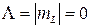, и состояния обозначаются .

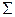Обе волновые функции молекулы водорода симметричны относительно любой плоскости, проходящей через ось молекулы, и обозначение соответствующих состояний дополняется верхним индексом «плюс»: Σ⁺. Функция Ψ_s симметрична по отношению к перестановке ядер, т.е. симметрична относительно центра инверсии, и обозначается Σ_g⁺, функция Ψ_а – антисимметрична относительно центра инверсии и обозначается Σ_u^+.

С учетом мультиплетности электронных состояний получаем:

а) основным электронным состоянием молекулы водорода является состояние ¹Σ_g⁺ с энергией Е_{1s ,} пространственное распределение электронной плотности в котором описывается функцией Ψ_s ;

б) первое возбужденное электронное состояние молекулы обозначается 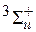, ему соответствует энергия Е_{1а ,} и пространственное распределение электронной плотности в этом состоянии описывается функцией Ψ _а (рисунок 21.3).

Воспользуемся формулами (21.12) и выразим плотность вероятности обнаружить электроны (т.е. электронную плотность) в окрестности ядер молекулы водорода:

Первые два слагаемых соответствуют плотности вероятности обнаружить каждый из электронов в отдельных атомах водорода. Третье слагаемое описывает дополнительную плотность вероятности, обусловленную перекрыванием Ψ-функций (Ψ_А(1)Ψ_В(1)) и (Ψ_А(2)Ψ_В(2)) электронов в межъядерной области.

Как видим, в состоянии, описываемом функцией Ψ_s, электронная плотность в межъядерной области увеличивается вследствие перекрывания Ψ-функций, что и приводит образованию химической связи.

В асимметричном состоянии молекулы (Ψ _а) электронная плотность в межъядерной области уменьшается по сравнению с электронной плотностью изолированных атомов; поэтому атомы отталкиваются, и химическая связь не образуется. Таким образом, информация, полученная об электронных переходах и электронных состояниях молекул, является основой для анализа природы химической связи в них.

[1] Приближение Борна – Оппенгеймера – вариация адиабатического приближения в квантовой механике, метод анализа молекулярных систем, заключающийся в том, что в системе выделяют и раздельно описывают ядра атомов и электроны, для которых характерные времена изменения состояния сильно различаются. Адиабатическое приближение – метод приближённого решения задач квантовой механики, применяемый для описания квантовых систем, в которых можно выделить быструю и медленную подсистемы. Исходная задача решается в два этапа: сначала рассматривается движение быстрой подсистемы при фиксированных координатах медленной подсистемы, а затем учитывается движение последней.

Дата добавления: 2014-01-13