
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рассмотрим пример декодирования
|
|
|
|
K j
N-(k-1)
K
N-1
r(n,k,s) = ∑ r(j, k-1, s-(j+1)) + r(0, k, s) (13).
j=0
Следствие 2:
r(n,k,s) = ∑ r(n-(j+1), k-j, s- jn +j(j+1)/2) (14).
j=0
Теорема 3. Для любых значений n,k,s справедливо:
r(n,k,s) = r(n, n-k, n(n+1)/2-s) (15).
Теорема 4. Для любых значений n,k,s справедливо:
r(n,k,s) = r(n, k, k(n+1)-s) (16).
Теорема 5. Для четных значений n илюбых k,s справедливо:
r(n,k,s) = ∑∑ r (n/2, k1, s1) r(n/2,k-k1, s-s1-(k-k1)n/2),
K1 s1
где 0 ≤ k1 ≤ k, s1min ≤ s1 ≤s1max, при этом: (17).
s1min=max{k1(k1+1)/2, s-(k-k1)(2n-(k-k1-1))/2}
s1max=min{nk1/2-k1(k1-1)/2, s-(k-k1)(n+k-k1+1)/2}
Замечание. Для нечетных n, а так же для любых неравных разбиений n -блока на подблоки (n1,n2), формула (17) преобразуется к виду: (18)
r(n,k,s) = ∑∑ r (n1, k1, s1) r(n2, k-k1, s-s1-(k-k1)n1),
K1 s1
в формуле для s1max n/2 заменяется на n1, а n на 2n1.
Теорема 6. Для любых значений n,k,s справедливо:
r(n,k,s) = ∑ r(n-i, k-1, s-ik) (19).
i=1
Следствие 3: Для любых значений r(n,k,s) имеет место рекуррентное соотношение:
r(n,k,s) = r(n-1,k-1,s-k)+ r(n-1,k,s-k) (20).
В ходе работы были предприняты попытки получить явные выражения для r(n,k,s). Оказалось, чтов общем виде, без использования специальных функций такие выражения получить невозможно. В случае использования, например, функций Гаусса, выражения становятся настолько громоздкими и труднореализуемыми, что не представляют практического интереса.
Тем, не менее, удалось получить явные выражения для частных случаев (k=2, k=3, k=4). Они могут использоваться для вычисления исходных значений r(n,k,s) c последующим применением рекуррентных соотношений.
r(n,2,s)=min{s-2;n-1}-max{ ](s-1)/2[;1}+1 (21).
r(n,3,s)=(2]s/3[+1-s)x + x2+(s-]s/3[-5/2)ξ- (22)
-ξ2/2-y(4](s-]s/3[)/2[-y-φ-7)/4-ψ, где:
x=[s/2-]s/3[], y=s-]s/3[-4,
ψ= { y-1- [(y-1)/2],если ( s-]s/3[)/2) целое,
0 в других случаях.
φ=y-1-2 [(y-1)/2],
ξ=min{s-4;n-1}-max{ ]s/3[;2 }+1
Явное выражение для k=4 приводить не будем из за его громоздкости, но оно вполне реализуемо.
Для того, что бы иметь возможность оценить объем памяти и вычислений, требуемых для реализации кодирования, необходимо знать при каких k и s, коэффициенты r(n,k,s) принимают наибольшие значения.
В связи с этим, сформулированы и доказаны следующие теоремы.
Теорема 7. Для любого k≤n, r(n,k,s) примет наибольшее значение при s = ]k(n+1)/2[.
Теорема 8. Для любого n, r(n,k,s) примет наибольшее значение при k =]n/2[, s =]]n/2[(n+1)/2[.
На основе этих соотношений получены алгоритмы, реализующие КТ, обеспечивающие минимальную трудоемкость реализации КТ при заданном значении n.
Выражения (12), (13) использовались для вычисления Rn(p), К сж для рассмотренных выше графиков.
Формула (14)использована для построения алгоритма нумерации.
Соотношения (15) и (16) устанавливают свойства симметрии для коэффициентов. Учет симметрии позволит экономить память, требующуюся для хранения коэффициентов при реализации кодирования, по крайней море, в 4 раза.
Теоремы 7 и 8 устанавливают величину объема памяти, требуемую для реализации КТ. Остальные соотношения будут использоваться для вычисления значений коэффициентов в различных вариантах реализации кодирования.
Совокупность рассмотренных соотношений представляют собой математический аппарат, необходимый и достаточный для реализации КТ.
Перейдем к построению нумерации.
Ранее было определено, что кодовое слово w, соответствующее n - блоку, это упорядоченная тройка двоичныхнаборов (k, s, b(n,k,s)). Следовательно, в ходе кодирования необходимо каждому элементу множестваRk, s поставить в соответствие номерb(n,k,s), причем 0 ≤ b(n,k,s) ≤ r(n,k,s) – 1.
При использовании для этой цели таблиц соответствия исходных блоков и кодовых слов, трудоемкость кодирования возрастает как экспоненциальная функция длины блока.
Очевидно, что эффективная реализация кодирования с такой трудоемкостью весьма затруднительна, даже с учетом достижений современной микроэлектроники и флэш-памяти.
Альтернативой является использование алгоритмов нумерации, когда b(n,k,s) определяется как целочисленная функция таких параметров блока, как раз разрядность, число единиц в блоке, номера их позиций.
Перейдем к построению алгоритма нумерации. Будем рассуждать следующим образом. Возьмем некоторый n -блок и зафиксируем номер k –ой единицы ik.
В этом случае остальные номера от 1 до (ik – 1) будут размещаться в (ik – 1) разрядной сетке и количество всех возможных комбинаций k номеров с суммой s, будет равно r (ik – 1, k, s).
Далее, зафиксируем номер ik-1. Остальные номера от 1 до ik-2 будут размещаться в (ik-1 – 1) разрядной сетке. В этом случае, количество всех возможных комбинаций (k - 1) номеров в (ik-1 – 1) разрядной сетке, c суммой s - ik будет равно r(ik-1 – 1, k - 1, s - ik).Аналогичные рассуждения проведем для всех прочих номеров до i1 включительно. В результате получим для каждого ij соответствующее значение r(ij – 1, j, s - ik- ik-1-…- ij+1).
Представляется логичным предположить, что:
b(n,k,s)=r(ik– 1,k,s)+r(ik-1– 1,k-1,s- ik)+ + r(ik-2– 1,k-2,s- ik-ik-1)+...+ r(i2 – 1, 2, s - ik- ik-1-...- i3)+ + r(i1 – 1, 1, s - ik- ik-1-...- i2)
Учтем, что s - ik- ik-1-...- i2 = i1, следовательно, r(i1 – 1, 1, s - ik- ik-1-...- i2) Ξ 0.
Кроме того, учтем, что s - ik- ik-1-...- i3 = i2+ i1, s - ik- ik-1-...- i4 = i3+ i2+ i1 и т.д.
Запишем нашу гипотезу следующим образом:
b(n,k,s) = r(ik – 1,k, ik+ ik-1+...+ i1)+ + r(ik-1 – 1,k-1, ik-1+ ik-2...+i1)+...+ r(i2 – 1, 2, i2+ i1 ) =
=∑ r (ij – 1, j, ∑ im)(22)
j=2 m=1
В ходе работы над методом были сформулированы и доказаны две теоремы подтверждающие справедливость гипотезы (22).
Теорема 9. Любой номер b(n,k,s), вычисленный по формуле (22) удовлетворяет неравенству: 0 ≤ b (n, k, s) ≤ r (n, k, s) – 1
Теорема 10. Между n-блоками и упорядоченными тройками чисел (k, s, b(n,k,s)), где b(n,k,s) определяется по формуле (22), существует взаимо однозначное соответствие.
В качестве примера рассмотрим нумерацию при n=11, k=4, s=25. В этом случае формула (22) преобразуется к виду:
b(11,4,25)=r(i4-1,4,25)+r(i3-1,3,25- i4)+ r(i2-1,2,25-i4- i3)
Запишем все возможные комбинации 4-х номеров позиций единиц, дающих в сумме 25 в 11 -разрядной сетке (Таблица 1). Видно, что каждой комбинации соответствует свой собственный номер, отличный от всех остальных.
Таблица 1. Пример нумерации
| I4 | I3 | I2 | I1 | Слагаемые формулы (22) | b(n,k,s) |
| r(10,4,25)+r(9,3,14)+r(2,2,4)=14+8+0 | |||||
| r(10,4,25)+r(8,3,14)+r(3,2,5)=14+6+1 | |||||
| r(10,4,25)+r(8,3,14)+r(2,2,5)=14+6+0 | |||||
| r(10,4,25)+r(7,3,14)+r(4,2,6)=14+4+1 | |||||
| r(10,4,25)+r(7,3,14)+r(3,2,6)=14+4+0 | |||||
| r(10,4,25)+r(6,3,14)+r(5,2,7)=14+1+2 | |||||
| r(10,4,25)+r(6,3,14)+r(4,2,7)=14+1+1 | |||||
| r(10,4,25)+r(6,3,14)+r(3,2,7)=14+1+0 | |||||
| r(10,4,25)+r(5,3,14)+r(4,2,8)=14+0+0 | |||||
| r(9,4,25)+ r(8,3,15)+r(4,2,6)= 6+6+1 | |||||
| r(9,4,25)+ r(8,3,15)+r(3,2,6)= 6+6+0 | |||||
| r(9,4,25)+ r(7,3,15)+r(5,2,7)= 6+3+2 | |||||
| r(9,4,25)+ r(7,3,15)+r(4,2,7)= 6+3+1 | |||||
| r(9,4,25)+ r(7,3,15)+r(3,2,7)= 6+3+0 | |||||
| r(9,4,25)+ r(6,3,15)+r(5,2,8)= 6+1+1 | |||||
| r(9,4,25)+ r(6,3,15)+r(4,2,8)= 6+1+0 | |||||
| r(9,4,25)+ r(5,3,15)+r(4,2,9)= 6+0+0 | |||||
| r(8,4,25)+ r(7,3,16)+r(6,2,8)= 1+2+2 | |||||
| r(8,4,25)+ r(7,3,16)+r(5,2,8)= 1+2+1 | |||||
| r(8,4,25)+ r(7,3,16)+r(4,2,8)= 1+2+0 | |||||
| r(8,4,25)+ r(6,3,16)+r(5,2,9)= 1+0+1 | |||||
| r(8,4,25)+ r(6,3,16)+r(4,2,9)= 1+0+0 | |||||
| r(7,4,25)+ r(6,3,17)+r(5,2,10)=0+0+0 |
Таким образом, сформулирован метод кодирования тройками (КТ), доказана его универсальность, разработан математический аппарат.
Для практической реализации КТ средствами вычислительной техники (программно или аппаратно) необходимо представить процессы кодирования и декодирования в виде вычислительных алгоритмов.
На Рис. 5 представлен алгоритм кодирования в соответствии со структурой кодового слова (9) и методом нумерации по формуле (22).
 А В
А В 



|
 1
1
|
|



 2
2 
|  | |||

 3
3
|
| ||||


 4
4
 | |||
| |||


|
|


|
 |  | ||
 7
7
|
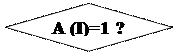
 нет
нет
 8
8

|



 да
да
 9 да
9 да



Рис. 5. Алгоритм кодирования
Считается заданным n - длинаблоков, на которые разбивается исходная последовательность двоичных символов (блок А1). Под I понимается номер обрабатываемого разряда текущего n -блока, k -текущее значение количества единиц в блоке, S - сумма номеров их позиций, b номер, вычисляемый по формуле (22), А(I) – содержимое I -го разряда n -блока.
В блоках А2, 3, 4, 5 значениям параметров кодового слова присваиваются исходные значения.
Пусть с выхода канала поступают последовательно двоичные данные. В блоке А6 осуществляется прием очередного бита этой последовательности. В блоке А7 значение I увеличивается на единицу.
В блоке А8 выясняется равно ли содержимое I -го разряда n -блока единице, и если «Да», то происходит вычисление соответствующего слагаемого формулы (22) (блоки А9, В1,2,3). В блоке В4 вычисленное слагаемое прибавляется к текущему значению номера b.
Если в блоке А8 выясняется, что содержимое I -го разряда n -блока равно нулю, то происходит переход на блок В5. Здесь выясняется все ли разряды n -блока проверены и если «нет», то осуществляется пёреход на блок А6. Если «да», то в блоке В6 происходит преобразование, в соответствия со вторым слагаемым выражения для длины кодового слова (22). То есть осуществляется передача не исходного S, а его номера.
В блоке В7 вычисляется коэффициент, необходимый для определения величины третьего слагаемого выражения для длины кодового слова(22). В блоке В8 происходят выдача сформированного кодового слова. Передается L бит. Если по завершению передачи очередного кодового слова, из канала продолжают поступать данные, осуществляется переход на блок А2.
На Рис. 6 представлен алгоритм декодирования.


 А В
А В

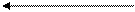


|
 |  | ||
 | 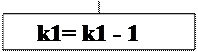 |

 3
3
|  | |||


 4 да
4 да
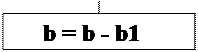 | |||
|


 5
5
|
|
|
|



 6
6




|
 8
8
|



 9
9




|


 10
10


 да
да
|


 да
да
 |
 Рис. 6.Алгоритм декодирования
Рис. 6.Алгоритм декодирования
Считается заданным длина n -блоков, на которые разбита последовательность двоичных символов перед применением КТ. Пусть было принято очередное кодовое слово (блок А2). Зная n, в соответствия с (22) определяем количество разрядов в кодовом слове, отводимое под k. Отсчитываем от начала кодового слова это количество и полученное двоичное число и есть k (блок АЗ).
Зная n и k, в соответствии с (22) (второе слагаемое) определяем количество двоичных разрядов, отводимое под номер S. Затем получаем истинное значение S.
S=S + k(k+1)/2-1
Все это выполняется в блоке А4.
Оставшиеся разряды кодового слова содержат номер b – блок А5. В блоке А6 происходит зануление В — одномерного массива разрядности n - бит, в котором, по окончании декодирования будет находиться исходный n -блок. В блоке А7 присваиваются исходные значения служебным переменным k1 и S1. Их смысл поясним далее.
Начиная с блока А8, происходят восстановление номеров позиций k единиц с суммой S. Операция — обратная вычислению b(n,k,s). Поясним принцип этой операции при помощи Таблицы 1. На основе известных номеров (четыре левых колонки) вычислялся номер b (правая колонка). Теперь же нам известен номер b, и нужно определять номера позиций единиц. Видно, что все возможные номера b(n,k,s) можно разбить на группы при помощи сравнения номеров и значений r(10,4,25),r(9,4,25), r(8,4,25) и т.д. Причем значения r(10,4,25) =14, r(9,4,25) = 6 и т.д., задают наименьшие номера этих групп, т.е. определяют границы групп. Можно заметить, что 4 и 25 это значения, соответственно k и S, а первый параметр первого коэффициента первой группы n1 (в таблице это 10) определяется по формуле:
n1 = min (n, s1-(k1-1) k1/2) – 1, (23)
где исходные значения k1 и S1 задаются в А7.
Формула аналогична (21). А смысл ее в поиске n1 наибольшего возможного номера при заданных значениях n,k,S без единицы, что соответствует ik - 1 в формуле (22). Пусть, например, b=16. n1 =min(11,25 – 4x3/2) – 1 = 10, (блок А8). Вычисляем b1 = r(10,4,25) =14, (блок А9). Сравниваем b и b1 (блок A10). Поскольку 16 > 14, b входит в первую группу, а i4 = 11 (блок В1) в соответствующий разряд В заносится 1 (блок В2).
Далее нужно перейти ко второму слагаемому формулы (22). Формируем новое значение k1 (блок В3) и проверяем все ли номера позиций определены (блок В4) и если нет - вычисляются новые значения b,S1,n (блоки В5, 6, 7) с переходом на А8 и т.д.
В нашем случае : k1 = 3 >1, b = 16-14 = 2, S1 = 25— 11 = 14. Далее выполняется описанная выше последовательность действий для нового номера b. Вычисляем n1 (блок А8). Затем, вычисляем b1 = r(9, 3, 14) = 8 (блок А9) Сравниваем b и b1 (блок А10). Поскольку 8 > 2 переходим на блок А11 с возвратом на А9 и т.д.
В итоге, в массиве В будет находиться исходный n -блок (блок В9). В блоке В10 происходят его выдача и в случае необходимости (блок В11) возврат на А1.
Для наглядности рассмотрим кодирование конкретного n - блока, пусть n= 50. Возьмем n -блок:
50 49 48 47 46...11 10 9 8 7 6 5 4 3 2 1
А = 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 0
После приема первого бита (блок А6), I становятся равным 1. Поскольку А (I) = 0, переходим на В5. Так как I<n переходим на А6. I = 2, А(I) = 1. В блоке В3 вычисляем значение r(1,1,2) = 0.
В блоке В4 прибавляем вычисленное значение к текущему значению b. Поскольку I<n переходим на А6 и т.д.
Далее вычисляем значения: r(2,2,5) = 0; r(З,З,9) =0; r(8,4,18) = 8.
Суммарный номер (блок В4) будет равен: b = 0 + 0 + 0 + 8 = 8. Как только I будет равно 50 (блок В5), перейдем на В6. К этому моменту k = 4, S = 18, b = 8. В блоке В6, S будет преобразовано: S = S – k (k+1)/2 + 1 = 9.
Далее вычисляем значение r (50,4,18) = 17. Теперь мы можем определить количество разрядов, отводимое в кодовом слове для каждого из трех параметров (см. (9)).
L=]log 2 51[+ ]log 2 185[+]log 2 17 [ =6 + 8 + 5 = 19.
Кодовое слово будет выглядеть:
W = 000100 00001001 01000
k = 4 S = 9 b = 8
Таким образом, в результате кодирования, вместо 50 символов, требуется 19.
В блоке В8 происходит выдача 19 символов, соответствующих кодовому слову. В случае необходимости, переходим на А2.
Для наглядности рассмотрим декодирование конкретного кодового слова, полученного в приведенном ранее примере.
Вычисляем ] log 2 51[= 6. Отсчитываем в кодовом слове слева это количество разрядов и получаем k = 000100 = 4 (блок АЗ). Таким образом, в исходном n —блоке есть 4 единицы. Далее вычисляем ] log 2 (4(50 – 4) + 1)[= 8. Отсчитываем 8 разрядов (начиная с 7 —го) и получаем S = 00001001 = 9. Получаем истинное значение S = 9 + 4x5/2 – 1 = 18 (блок А4). Следовательно, исходный блок содержит 4 единицы с суммой позиций 18.
Номер конкретного n – блока из всех имеющих данные k и S записан в последних 5 разрядах.
b = 01000 = 8 (блок А5).
В соответствии с (23) (блок А8):
n1 = min (50, 18 – 3x4/2) - 1 = 11.
Далее вычисляем b1 = r(12,4,18) = 20, (блок А9). Сравниваем b и b1: 8 < 20, поэтому n = 11 (блоки АI0, А11) и переход на А9:
b1 = r (11, 4, 18) = 19 и т.д.
b1 = r (10, 4, 18) = 18
b1 = r (9, 4, 18) = 11
Далее:
b1 = r (8, 4, 18) = 8.
Условие блока АI0 выполняется: I = 9 (блок В1) и b(9) = 1 (блок В2). k1 = k1 – 1 = 3 > 1 (блоки ВЗ, В4), b = 8 – 8 = 0, S1 = 18 – 9 = 9, n = 49 блоки (В5, В6, В7) и переход на А8.
n1 = min (49, 9 – 2x3/2) – 1 = 5 (А8):
b1 = r (6, 3, 9) = З.
Сравниваем b и b1: 0 < 3, n1 = 5
b1 = r (5, 3, 9) = 2
b1 = r (4, 3, 9) = 1
И наконец:
b1 = r (3, 3, 9) = 0
i = 4 (B1), b (4) = 1, k1 = 2 > 1, b = b – b1 = 0,
S1 = 9 – 4 = 5, n = 48, переход на А8:
n1 = min (48, 5 – 1x2/2) – 1 = 4,
b1 = r (4, 2, 5) = 2 > b
b1 = r (3, 2, 5) = 1 > b
b1 = r (2, 2, 5) = 0 = b → i = 3, b (3) = 1, k1 = 1;
b = 0, S1 = 5 – 3 = 2, n = 47, переход на А8.
n1 = min (47, 2 – 0x1/2) – 1 = 1
b1 = r (1, 1, 2) = 0 = b
i = 1 + 1 = 2, b (2) = 1, k1 = 0 <1, переход на В9.
В результате, в массиве блока В9 должен находиться исходный n - блок. Мы получили, что b(9), b(4), b(3) и b(2) равны 1, остальные 0 (блок А6).
50 49 48 47........10 9 8 7 6 5 4 3 2 1
В= 0 0 0 0..........0 1 0 0 0 0 1 1 1 0
Сопоставив значение содержимого В с n – блоком примера кодирования можно убедиться, что декодирование проведено верно.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 280; Нарушение авторских прав?; Мы поможем в написании вашей работы!