Лекция 46-47. Положительные числовые ряды. Интегральный признак сходимости. Знакочередующиеся ряды. Теорема Лейбница

Интегральный признак Коши. Этот признак состоит в следующем. Если члены a_n положительного ряда 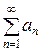монотонно убывают, то этот ряд и несобственный интеграл 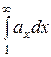сходятся или расходятся одновременно. Здесь 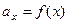- непрерывная монотонно убывающая функция, принимающая при x = n значения a_n членов ряда.

Доказательство интегрального признака Коши, как и признаков Даламбера и Коши опустим. Это доказательство, кстати, использует в принципе ту же геометрическую идею, что была применена при доказательстве расходимости гармонического ряда.

Пример 1. Исследуем на сходимость – расходимость обобщенный гармонический ряд:

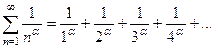(1)

При 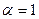мы получаем гармонический ряд, который, как мы доказали, расходится. При 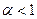ряд (1) тем более будет расходиться, так как его члены больше членов гармонического ряда. Осталось исследовать случай . Применим к ряду (1) при интегральный признак Коши. Для этого вычислим несобственный интеграл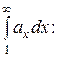

.

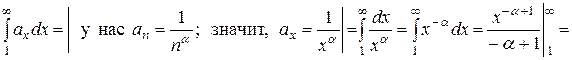
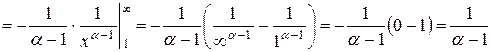В результате получили конечное число 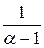. Таким образом, сходится. Но тогда, по интегральному признаку Коши, сходится и ряд (1). То есть

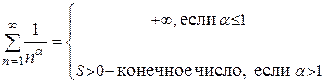(2)

Дата добавления: 2014-01-13