Теорема Вейерштрасса

а) Пусть значения x_n переменной x монотонно возрастают и при этом все они меньше некоторой постоянной величины C. Такая переменная x называется монотонно возрастающей и ограниченной сверху (числом C). Она заведомо имеет конечный предел a, причем .

б) Пусть значения x_n переменной x монотонно убывают и при этом все они больше некоторой постоянной величины C. Такая переменная x называется монотонно убывающей и ограниченной снизу (числом C). Она заведомо имеет конечный предел a, причем 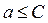. 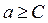Наглядную иллюстрацию этой ситуации дает рис. 3.3.

Однако сходимость ряда еще не доказана. Мы доказали только, что последовательность «четных» частичных сумм имеет пределом число s. Осталось доказать, что «нечетные» частичные суммы также стремятся к пределу s.

2. Рассмотрим теперь частичную сумму S_2m+1 ряда (3) с нечетным числом слагаемых: S_2m+1= S_2m + a_2m+1. Тогда, согласно (7) и (4),

(8)

Таким образом, и при четных, и при нечетных значениях номера n для частичных сумм S_n знакочередующегося ряда (3) имеем:

- число, причем 0 < S < a₁ (9)

А это и означает, что S – сумма ряда (3), причем 0 < S < a₁. Признак Лейбница доказан.

Примечание. Признак Лейбница позволяет не только устанавливать сходимость – расходимость знакочередующегося ряда (3), но и позволяет, при условии его сходимости, находить сумму S с любой заданной точностью. Действительно, сложив в ряде (3) какое-либо число N его первых слагаемых и отбросив остальные, мы фактически отбросим знакочередующийся ряд, начинающийся со слагаемого a_N+1, сумма которого, по признаку Лейбница, не будет превосходить этого первого отброшенного слагаемого. Значит, и ошибка при вычислении суммы S знакочередующегося ряда не будет превосходить первого из отброшенных слагаемых этого ряда. Этим обстоятельством широко пользуются для приближенного нахождения сумм сходящихся знакочередующихся рядов с нужной точностью.

Пример 2. Показать, что знакочередующийся ряд

(10)

сходится, и найти его сумму S с точностью до 0,01.

Решение. Данный ряд сходится по признаку Лейбница. Для нахождения его суммы S с точностью 0,01 найдем первое из слагаемых этого ряда, по абсолютной величине меньше 0,01. Это, очевидно, пятое слагаемое . Отбрасывая его и остальные, следующие за ним, слагаемые, получим:

Дата добавления: 2014-01-13