Упражнения. 1. С помощью интегрального признака Коши исследовать на сходимость ряд а)

1. С помощью интегрального признака Коши исследовать на сходимость ряд а) 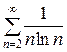. Ответ: Расходится. б) . Ответ. Расходится.

в) . Ответ. Сходится.

2. Исследовать на сходимость следующие знакочередующиеся ряды с помощью признака Лейбница:

а) 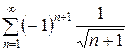. Ответ. Сходится. б) . Ответ. Расходится.

3. Исследовать на сходимость знакочередующийся ряд

.

В случае сходимости выяснить, сходится он абсолютно или условно, а также найти его сумму S с точностью 0,1.

Ответ: ряд сходится абсолютно; .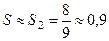

4. Показать, что сумма S условно сходящегося ряда

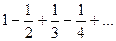
увеличится в полтора раза, если после каждых двух положительных его слагаемых поместить одно отрицательное.

Функциональные ряды (общие положения)

Определение 1. Ряд вида

, (19)

слагаемыми которого являются функции, называется функциональным.

Если зафиксировать аргумент x, то каждая функция станет числом, а ряд (19) станет числовым рядом. При одних значениях x этот ряд может оказаться сходящимся, при других – расходящимся.

Определение 2. Областью сходимости функционального ряда (19) называется множество всех тех значений x, при которых ряд сходится. Остальные значения x составляют его область расходимости.

Нас, естественно, в первую очередь будут интересовать области сходимости функциональных рядов, а также суммы рядов в их областях сходимости.

Пусть D – область сходимости данного функционального ряда (19). На практике область D может выглядеть по-разному: быть промежутком или интервалом оси ox, представлять собой всю ось ox или единственную ее точку, даже быть пустым множеством (последний случай – неинтересный). Для каждого x є D этот ряд имеет конечную сумму S=f(x):

(x є D) (20)

При исследовании любого функционального ряда встают две основные задачи:

1) Определение его области сходимости D.

2) Определение его суммы f (x) для (x є D). (21)

Не менее интересна и обратная проблема: подобрать такой функциональный ряд из возможно более простых слагаемых u_n(x), чтобы он в своей области сходимости D имел сумму, совпадающую с заданной функцией f (x) (то есть чтобы выполнялось равенство (20)). Эта проблема называется проблемой разложения заданной функции f (x) в функциональный ряд. Качество решения этой проблемы будет тем выше, чем проще подберется этот ряд; чем быстрее он будет сходиться; тем шире будет его область сходимости D.

Важность решения этой проблемы очень велика. Ведь разлагаемая в функциональный ряд (20) функция f (x) может быть сложной и даже не выразимой через элементарные функции. Например, она может быть первообразной для некоторой функции g (x), для которой неопределенный интеграл

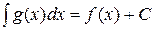
является неберущимся. А слагаемые u_n(x) функционального ряда (20), сумма которого будет равна f (x), могут, наоборот, оказаться достаточно простыми элементарными функциями, легко анализируемыми и вычисляемыми. Поэтому получив разложение

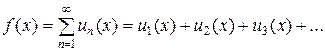(x є D) (22)

нужной нам функции f (x) в такой функциональный ряд, мы в итоге получим возможность для x є D оперировать не с самой функцией f (x), а с ее составляющими u₁ (x), u₂ (x), …, которые и проще, и удобнее самой функции.

Пример 5. Рассмотрим функциональный ряд

Этот ряд сходится при всех значениях х в интервале (-1,1), т.е. при всех х, удовлетворяющих условию , поскольку он будет геометрической прогрессией со знаменателем меньше 1. Для каждого значения х в интервале (-1,1) сумма ряда равна . Таким образом, в интервале (-1,1) данный ряд определяет функцию 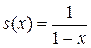, которая является суммой ряда, т.е.

Обозначим через сумму первых n членов ряда (19). Если этот ряд сходится и сумма его равна s(x), то

,

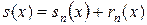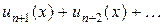где есть сумма ряда , т.е. .

В этом случае величина - называется остатком ряда. Для всех значений х в области сходимости ряда имеет место соотношение 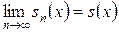, поэтому . Т.е. остаток сходящегося ряда стремится к нулю при .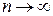

В следующей лекции задачи (21) и (22) будут рассмотрены для двух наиболее простых и важных типов функциональных рядов:

1) Для степенных рядов вида

(23)

2) Для обобщенных степенных рядов вида

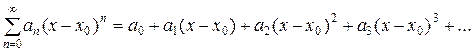(24)

Дата добавления: 2014-01-13