Лекция 48. Понятие о степенных рядах. Интервал сходимости степенного ряда. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена. Примеры разложения функций в ряды

Определение 1. Степенным рядом называется функциональный ряд вида

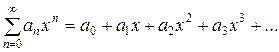(1)

где а₀,а₁,а₂,…, а_n – постоянные числа, называемые коэффициентами ряда.

Ряд вида

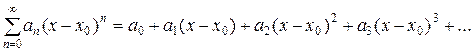(2)

также является степенным рядом. Это – степенной ряд, расположенный по степеням двучлена (x-a). Еще такой ряд называют обобщенным степенным рядом.

Начнем с того, что найдем область сходимости степенного ряда (1). Для этого проанализируем положительный числовой ряд, составленный из его модулей:

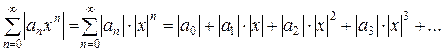(3)

Применим к нему признак Даламбера. Для этого найдем q:

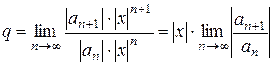; (4)

Введем обозначение

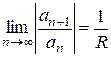, откуда 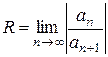(5)

Тогда выражение для q примет вид:

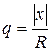(6)

Согласно признака Даламбера:

1) Если q <1, то есть если | x | < R, или, что одно и то же, если – R < x < R, то ряд (3) сходится. А вместе с ним сходится, причем абсолютно, и ряд (1).

2) Если q >1, то есть | x|>R или, что одно и то же, если x > R или x < –R, то ряд (3) расходится. Заметим, что при этом и ряд (1) тоже не будет сходиться, ибо условие 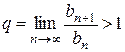для любого положительного ряда 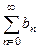означает, что начиная с некоторого номера N, то есть при n >N, отношение 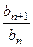становится больше 1 и остается таковым для любых n >N. А это значит, что для n >N будет 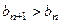. То есть начиная с номера N члены 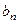положительного ряда 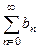растут, а значит, заведомо не стремятся к нулю. Получается нарушенным необходимое условие сходимости ряда 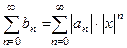, а заодно – и степенного ряда 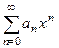, ибо слагаемые первого из них – просто модули последнего. То есть действительно при x > R и x < –R ряд (1) будет расходиться.

3) Наконец, если q = 1, то есть если x = ± R, то о сходимости – расходимости и ряда (3), и ряда (1) ничего сказать нельзя. Этот случай нужно исследовать особо.

Итак, выводы:

Степенной ряд (1) сходится при –R < x < R; расходится при x > R и x < – R; при x = ± R он может как сходиться, так и расходиться (рис.1).

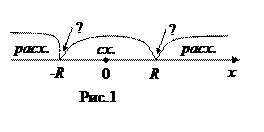Величина R, определяемая по формуле (5), называется радиусом сходимости степенного ряда (1). А интервал (- R; R) называется интервалом сходимости этого степенного ряда. Областью сходимости D степенного ряда (1), таким образом, является его интервал сходимости (- R; R) и, возможно, его концы. Этот интервал, в частности, может вырождаться в точку.

Пример 1. Найти область сходимости степенного ряда .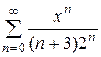

Решение. Данный ряд – это ряд вида (1) при 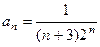. Определим, используя формулу (5), его радиус сходимости R:

.

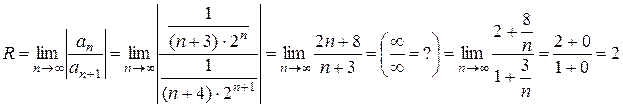Итак, данный степенной ряд сходится при x є (- 2; 2) и, возможно, еще в точках x = ± 2. Для всех остальных x он расходится.

Исследуем ряд при x = ± 2.

1) Если x = 2, то наш ряд примет вид:

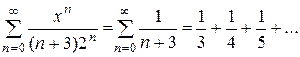
Это – гармонический ряд без первых двух своих членов. А значит, он расходится.

2) Если x = - 2, то получим:

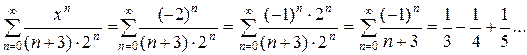
Это – знакочередующийся ряд, сходящийся по признаку Лейбница.

Таким образом, областью сходимости D степенного ряда 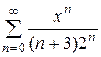является полуинтервал [- 2; 2).

Степенные ряды (1) обладают замечательным свойством: внутри их интервалов сходимости (- R; R) их можно почленно дифференцировать и интегрировать. Это значит, что если

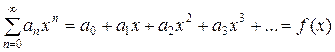, (- R < x < R) (7)

то

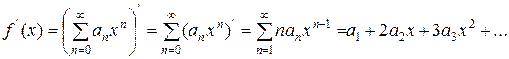
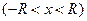; (8)

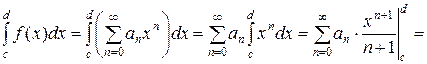
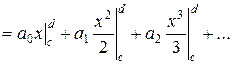
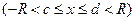. (9)

Эти факты примем без доказательства. Ограничимся лишь приведением примеров их использования.

Пример 2. Рассмотрим степенной ряд

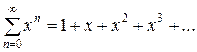(10)

Это – степенной ряд вида (1) при 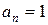(n = 0, 1, 2, …). Его радиус сходимости R, согласно формуле (5), равен 1: R = 1. То есть ряд (10) сходится в интервале (-1; 1), причем на обоих концах этого интервала он, очевидно, расходится. А так как этот ряд представляет собой еще и сумму бесконечной геометрической прогрессии со знаменателем x, то известна и его сумма:

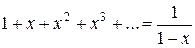
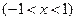(11)

Заменяя в (11) x на - x, получим еще один степенной ряд с известной суммой:

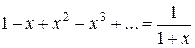
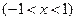(12)

Если теперь почленно продифференцировать равенства (11) и (12), то получим еще два разложения:

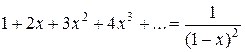
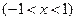(13)

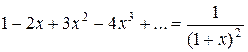
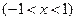(14)

А если равенство (12) почленно проинтегрировать в промежутке [0; t ], где 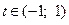, то получим:

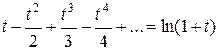
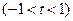(15)

Или в обычных обозначениях (заменив t на x):

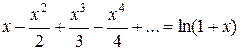
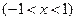(16)

Перейдя в этом равенстве к пределу при x ®1, получим:

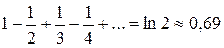(17)

Равенства (11) – (16) являются разложениями в степенные ряды, расположенные слева, тех функций, которые находятся справа.

Рассмотрим теперь общую проблему разложения любой заданной функции f(x) в степенной ряд (1). Для этого обратимся к формуле Маклорена:

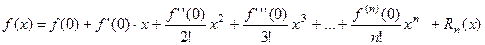(18)

Здесь

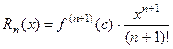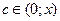, (19)

- остаточный член формулы Маклорена, записанный в форме Лагранжа.

Допустим, что функция f(x) имеет при x = 0 производные любого порядка. И допустим, что для некоторого множества значений аргумента x 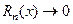при 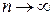. Тогда переходя в формуле Маклорена (18) к пределу при 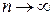, для этих значений x получим:

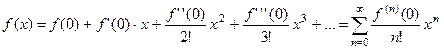(20)

Формула (20) представляет собой не что иное, как разложение функции f(x) в степенной ряд. Этот ряд называется рядом Маклорена. Разложение (20) верно и может быть использовано лишь для тех x, для которых 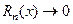при .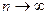

Пример 3. Пусть 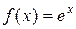. Тогда 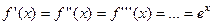, а значит, 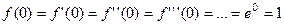. Разложение Маклорена (20) в данном случае примет вид:

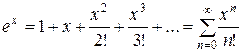(21)

Выясним теперь, для каких значений x оно справедливо. Для этого выпишем и проанализируем остаточный член 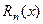. Так как 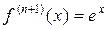при любом n, то

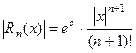
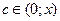(22)

Покажем, что 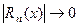при 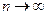для любого 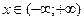. Для этого рассмотрим положительный числовой ряд 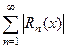. Применим к нему признак Даламбера:

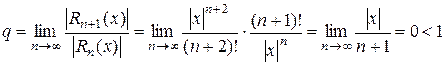(23)

- при любом x. Значит, ряд 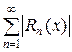сходится при любом x. Но тогда, в силу необходимого условия сходимости любого ряда, 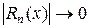при 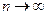. И это выполняется для любых x, 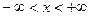. Значит, и разложение (21) справедливо для любых x:

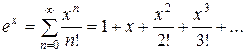
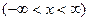(24)

Совершенно аналогично можно доказать и много других разложений различных функций в степенной ряд Маклорена. Например:

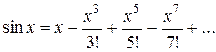
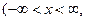х – в радианах) (25)

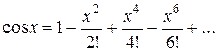
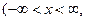х – в радианах) (26)

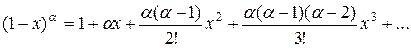
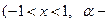любое) (27)

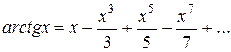
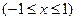(28)

Разложения (24) – (28) и им подобные широко используются как для приближенного вычисления значений стоящих слева функций с любой заданной точностью, так и для различных математических операций с указанными функциями.

Пример 4. Вычислить 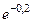с точностью до 0,0001.

Решение. Используя разложение (24) при х = - 0,2, получим:

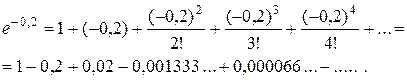
Отбрасывая в получившемся знакочередующемся ряде четвертое слагаемое, меньшее допустимой погрешности 0,0001, и все последующие за ним, которые еще меньше, получим с требуемой точностью:

.

Пример 5. Вычислить приближенно с точностью до 0,001 неберущийся определенный интеграл .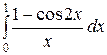

Решение. Используя разложение (26), получим:

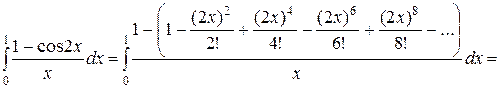
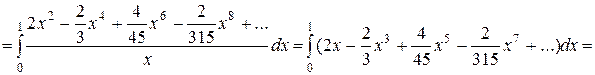
Отбрасывая в получившемся знакочередующемся числовом ряде четвертое слагаемое, которое меньше допустимой погрешности 0,001, и все последующие за ним, получим с требуемой точностью 0,001:

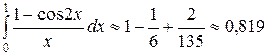. (29)

Пример 6. Построить в виде степенного ряда приближенное решение задачи Коши

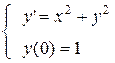(30)

Эта задача, заметим, не имеет точного решения, так как дифференциальное уравнение 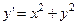не может быть решено в квадратурах.

Решение. Искомое решение 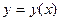ищем в виде ряда Маклорена:

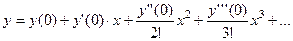
(31)

Для неизвестных коэффициентов 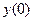, , 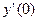, 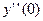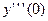… этого ряда получаем:

1) 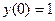- согласно начальному условию задачи Коши (30).

2) 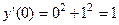согласно обоим равенствам задачи Коши (30).

3) Дифференцируя обе части уравнения 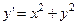, получим: 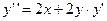. Полагая здесь х = 0 и учитывая, что 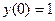и 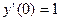, получим: ;

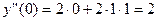4) Дифференцируя обе части равенства 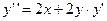, получим: , откуда .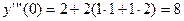

Продолжая этот процесс, можем получить 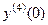; 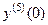, и т.д. В итоге на основании (31) искомое решение 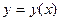задачи Коши (30) примет вид:

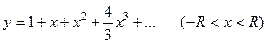(32)

На основании общей теории дифференциальных уравнений можно доказать, что ряд (32) сходится для всех 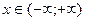. То есть его радиус сходимости 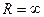. Ограничиваясь найденными первыми четырьмя слагаемыми этого ряда, получим следующее приближенное решение задачи Коши (30):

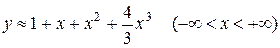(33)

Оно будет тем точнее, чем ближе х к нулю.

Дата добавления: 2014-01-13