Проверка статистических гипотез о законе распределения

Критерием согласия называется случайная величина

,

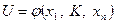где 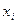- значение выборки, которая позволяет принять или отклонить гипотезу о предполагаемом законе распределения.

Алгоритм проверки гипотезы при помощи критерия согласия :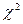

1. Построить интервальный статистический ряд вероятностей и гистограмму.

2. По виду гистограммы выдвинуть гипотезу

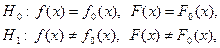
где 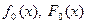- плотность и функция гипотетического закона распределения.

3. Используя метод моментов или максимального правдоподобия, определить оценки неизвестных параметров 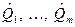гипотетического закона распределения.

4. Вычислить значение критерия по формуле

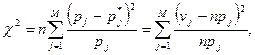(54.18)

где - теоретическая вероятность попадания случайной величины в j- й интервал при условии, что гипотеза верна:

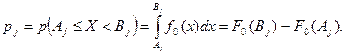(54.19)

Замечания. При расчете и 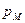в качестве крайних границ первого и последнего интервалов ,следует использовать теоретические границы гипотетического закона распределения. Например, для нормального закона ,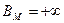. После вычисления всех вероятностей 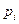проверить, выполняется ли контрольное соотношение

5. Из таблицы 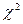(см. приложение) выбирается значение 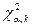, где α - заданный уровень значимости 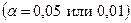, а k - число степеней свободы, определяемое по формуле

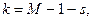
где s - число параметров гипотетического закона распределения, значения которых были определены в п. 3.

6. Если 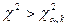, то гипотеза отклоняется, в противном случае нет оснований ее отклонить.

Последовательность действий при проверке гипотезы о законе распределения при помощи критерия согласия Колмогорова следующая.

1. Построить вариационный ряд и график эмпирической функции распределения 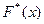(см. (54.1)).

2. По виду графика 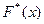выдвинуть гипотезу:

где 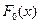- функция гипотетического закона распределения.

3. Используя метод моментов или максимального правдоподобия, определить оценки неизвестных параметров 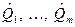гипотетического закона распределения.

4. Рассчитать 10−20 значений функции 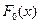и построить ее график в одной системе координат с функцией .

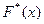5. По графику определить максимальное по модулю отклонение между функциями 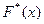и .

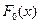(54.20)

6. Вычислить значение критерия Колмогорова

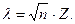(54.21)

7. Из таблицы распределения Колмогорова (см. приложение 2) выбрать критическое значение 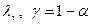. Здесь - заданный уровень значимости .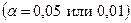

8. Если , то нулевая гипотеза отклоняется, в противном случае нет оснований ее отклонить.

Пример 54.8. Выдвинуть гипотезу о законе распределения случайной величины X и проверить ее с помощью критерия 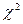. Вариационный ряд, интервальные статистические ряды вероятностей и гистограммы распределения случайной величины X приведены в примере 54.2. Уровень значимости равен 0,05.

Решение. По виду гистограмм, приведенных в примере 54.2, выдвигаем гипотезу о том, что случайная величина X распределена по нормальному закону:

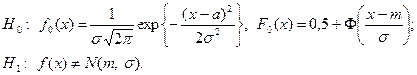
Используя метод моментов, определим оценки неизвестных параметров m и гипотетического (нормального) закона распределения:

.

Значение критерия вычисляем по формуле (54.18):

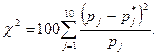
При проверке гипотезы используем равновероятностную гистограмму. В этом случае

Теоретические вероятности 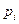рассчитываем по формуле (54.19)

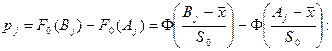
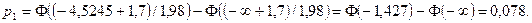
После этого проверяем выполнение контрольного соотношения

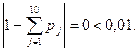
Тогда

После этого из таблицы распределения 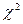выбираем критическое значение . Так как , то гипотеза принимается (нет основания ее отклонить).

Пример 54.9. По критерию Колмогорова проверить гипотезу о равномерном законе распределения случайной величины по выборке объема 10: 2,68 1,83 2,90 1,03 0,90 4,07 5,05 0,94 0,71 1,16, уровень значимости .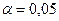

Решение. Вариационный ряд данной выборки имеет вид:

0,71 0,90 0,94 1,03 1,16 1,83 2,68 2,90 4,07 5,05.

После этого строим график эмпирической функции распределения 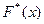(рис. 54.4).

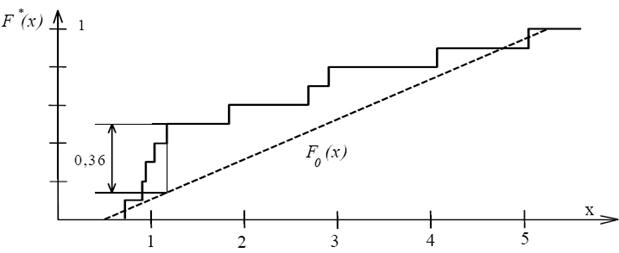
Рис. 54.4

Теоретическая функция распределения 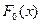равномерного закона равна

.

Максимальная разность по модулю между графикам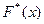и и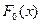

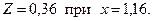
Вычислим значение критерия Колмогорова .

Из таблицы Колмогорова выбираем критическое значение 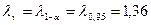. Так как , гипотеза о равномерном законе распределения принимается.

Дата добавления: 2014-01-13