Симплекс-метод розв’язку задачі ЛП

Лекція 2

Тема 1. Лінійне програмування

(8 г. – 4 лекції)

(2 г.)

2.2.2 Симплекс-метод розв’язку задачі ЛП

2.2.3 Метод штучного базису

2.2.4 Модифікований симплекс-метод(на самопідготовку)*

Сенс симплекс-методу полягає в переході від одного базисного рішення до іншого, при якому значення цільової функції зростає (за умови, що дана задача має оптимальний план і кожний її опорний план є невиродженим). Такий перехід можливий за умови відомості будь-якого опорного плану.

Запишемо умову задачі:

за умов

().

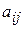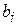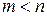Тут , та () – задані константи (та ).

Або у векторній формі: за умов (15)

, (16)

(), де (17)

,,,, …,,.

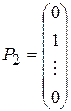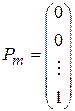Так як ,

то за визначенням опорного плану 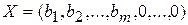є опорним планом даної задачі (останні 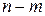компонент вектора дорівнюють нулю). Даний план визначається системою одиничних векторів 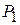, , 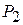…, , 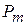які створюють базис 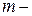вимірного простору. Тому кожен з векторів, а також вектор 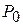можуть бути представлені у вигляді лінійної комбінації векторів даного базису. Нехай

().

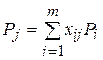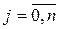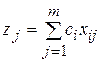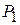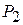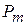Положимо (); (). Так як вектори , , …, - одиничні, то і , а

.

Теорема 5. (Ознака оптимальності опорного плану). Опорний план 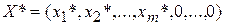задачі (15)-(17) є оптимальним, якщо для .

Теорема 6. Якщодля деякого 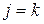і серед чисел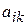 нема позитивних , то цільова функція (15) задачі (15)-(17) необмежена на множині її планів.

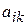Теорема 7. Якщо опорний план задачі (15)-(17) не вироджений та , але серед чисел є позитивні (не всі ), то існує опорний план 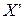такий, що .

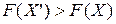Сформульовані теореми дозволяють перевірити наявний план на оптимальність та виявити доцільність переходу до нового опорного плану.

Приклад 3 [3]. Для виготовлення різних типів виробів А, В та С підприємство використовує три різних типи сировини. Норми витрат сировини на виробництво одного виробу кожного виду, ціна одного виробу А, В та С, а також загальна кількість сировини кожного виду, яке може бути використано підприємством, наведені у табл.:

Вид сировини	Норми затрат сировини (кг) на один виріб	Загальна кількість сировини (кг)
А	В	С
I II III
Ціна одного виробу (грн.)

Скласти план виробництва, при якому загальна ціна всієї виробленої продукції є максимальною.

Розв’язок.

1. Складаємо математичну модель задачі.

(18)

.

2. Запишемо задачу (15) у канонічній формі.

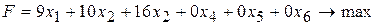
(19)

.

Додаткові змінні за економічним смислом означають кількість сировини того, чи іншого типу, що не використовується при даному плані виробництва. Наприклад, 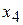– кількість сировини 1-го виду, що не використовується при виробництві.

Перетворену систему рівнянь запишемо у векторній формі:

де

; ; ; ; ; ; .

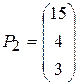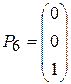Оскільки серед векторів є три одиничних, то для даної задачі можна безпосередньо записати опорний план:

3. Складаємо симплекс-таблицю для 1-ї ітерації.

3.1 Розраховуємо значення 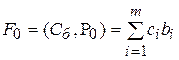, де :

,,

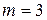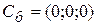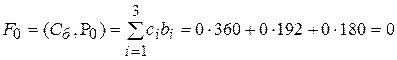
3.2 Розраховуємо , .

; ;

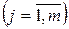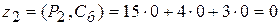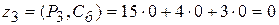
3.3 Розраховуємо оцінки .

; ; .

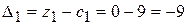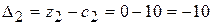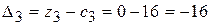Для векторів базису .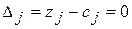

Так як для всіх змінних 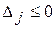, то план не є оптимальним.

4. Вибираємо роздільний стовпчик за правилом для визначення змінної, яку буде включено до базису.

. Це означає, якщо включити в план випуску продукцію виду С, то загальна ціна на продукцію збільшиться на 16 ум.од. Таким чином, до базису вводимо вектор .

5. Вибираємо роздільний рядок для визначення базисної змінної, яку буде виключено з базису. Для цього находимо 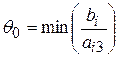для 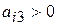. Тобто . Тобто, роздільним рядком є другий. Таким чином, з базису виключається вектор 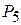, а вектор вводиться до базису.

6. Переписуємо симплекс-таблицю і перераховуємо її елементи наступним чином:

6.1 Елементи роздільного рядка отримуємо з елементів попередньої таблиці шляхом ділення їх на роздільний елемент. При цьому у стовпчику 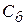записується коефіцієнт 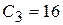, що стоїть у стовпчику вектору, який вводиться у базис.

6.2 Заповнюємо елементи стовпчиків для векторів, що входять до нового базису. В цих стовпчиках на перетині рядка та стовпчика однойменних векторів проставляємо одиниці, а всі інші заповнюємо нулями.

6.3 Всі інші елементи обчислюємо за правилом прямокутника (або за рекурентними формулами).

	Базис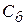
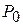
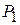
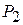
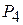
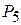
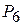
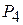
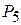
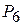
				-9	-10	-16

	Базис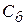
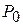
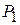
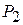
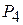
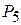
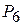
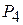
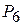
				¾ 11/4	½ 3/2 -2			-3/2 1/8 -3/8

	Базис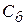
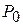
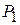
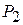
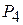
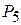
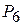
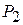
				¼ 5/4			1/9 -1/18 -1/6 2/9	-1/6 5/24 -1/8 5/3

На третій ітерації отримуємо оптимальний план 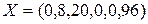при якому ум.од.

Аналіз розв’язку дає можливість зробити наступні висновки: оптимальний план випуску продукції передбачає випуск 8 виробів В та 20 виробів С. При цьому повністю використовується сировина 1-го та 2-го видів і залишається невикористаним 96 кг сировини 3-го виду.

Дата добавления: 2014-01-13