Времени и топлива

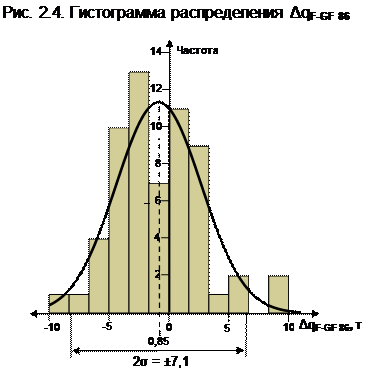
Взаимосвязь (корреляция) между погрешностями расчета

Точность расчета топлива

Разница между фактическим расходом топлива и топливом, рассчитанным по GF без учета КЗТ дана в табл. 4.

Таблица 4

Δq _{F-GF 86} = q _F86 -q _GF86

№ п.п	ΔqF-GF кг	Частота	Процент	№ п.п	ΔqF-GF, кг	Частота	Процент
	-8573		1,6		-1143		1,6
	-8111		1,6		-934		1,6
	-6061		1,6		-810		1,6
	-5467		1,6		-692		1,6
	-5399		1,6		-221		1,6
	-5183		1,6		-191		1,6
	-4752		1,6				1,6
	-4725		1,6				1,6
	-3899		1,6				1,6
	-3767		1,6				1,6
	-3754		1,6				1,6
	-3680		1,6				1,6
	-3669		1,6				1,6
	-3642		1,6				1,6
	-3396		1,6				1,6
	-3348		1,6				1,6
	-3158		1,6				1,6
	-3033		1,6				1,6
	-2912		1,6				1,6
	-2905		1,6				1,6
	-2791		1,6				1,6
	-2671		1,6				1,6
	-2452		1,6				1,6
	-2339		1,6				1,6
	-2319		1,6				1,6
	-2054		1,6				1,6
	-1995		1,6				1,6
	-1816		1,6				1,6
	-1791		1,6				1,6
	-1349		1,6				1,6
							1,6
Итого:		100,0

Итоговые данные представлены в табл. 5.

Таблица 5

Параметр	ΔqF-GF 86
Количество участков полета
Минимум, т	-8,6
Максимум, т	9,6
Сумма ΔqF-GF 86, т	-52.0
Среднее (мат. ожидание), т	-0,85
2σ (95%), т	±7,1
Пределы точности, т	-8,0÷6,3
Средний расход топлива, т	45,9
Относительная погрешность, %	15,2

Коэффициент двумерной корреляции устанавливает зависимость между парой случайных величин.

Значение К	Интерпретация
	взаимосвязь отсутствует
до 0.2	очень слабая взаимосвязь
до 0.5	слабая взаимосвязь
до 0.7	высокая взаимосвязь
до 0.9	очень высокая взаимосвязь
	пропорциональная линейная зависимость

Коэффициент двумерной корреляции определяется по формуле;

.

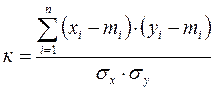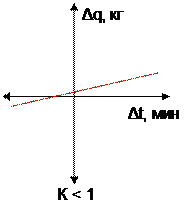
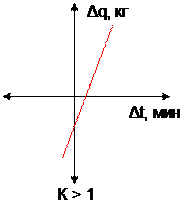
Графическое отображение коэффициента корреляции для оценки точности решения ТВЗ дано на рис. 2.5.

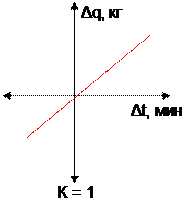Рис. 2.5. Графическое отображение коэффициента корреляции

Применительно для анализа точности решения ТВЗ получим:

.

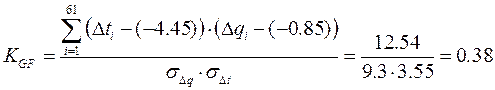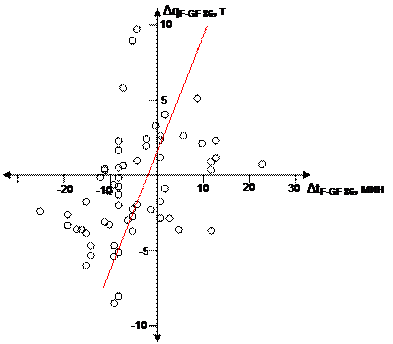
Коэффициент корреляции (K_GF) по результатам оценки точности решения ТВЗ соответствует 0,38, что указывает на очень слабую взаимосвязь. Наличие слабой взаимосвязи подтверждается рассеиванием величин, представленным на рис.2.6.

		Рис. 2.6. Рассевание величин ΔtF-GFиΔqF-GF 86 86,

Функция f(x) позволяет определить вероятность попадания случайной вели­чины Х на заданный участок от α до β:

.

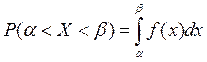Расширяя пределы интегрирования от -∞ до +∞, получаем важное соотно­шение:

.

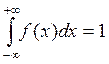Геометрически это означает, что площадь под кривой и осью ох, всегда равна единице.

В навигации часто требуется определить вероятность уклонения ВС от оси ЛЗП. В этом случае принимается предел интегрирования α = 0, а β = х, где х величина уклонения от ЛЗП. Для данного случая получим функцию Ф(х), которая называется функцией Лапласа. Она имеет вид:

.

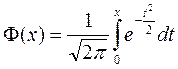Таблица значений функции Лапласа табулирована виде таблиц. С помощью таблицы можно подсчитать вероятность случайной величины в заданный интервал. Формула расчета имеет вид:

,

где: 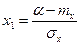, а .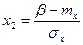

α – левая граница, β – правая граница трассы.

При этом следует учитывать, что Ф(-х) = - Ф(х).

Дата добавления: 2014-01-13