Построение кумуляты

Построение полигона

Берутся значения гистограммы.

Два варианта построения:

Рисунок 9.1

рис. 3,2

Можно построить полигон по средним значениям интервала

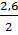= 1,3

2 + 1,3 = 3,3

4,6 + 1,3 = 5,9

7,2 + 1,3 = 8,5

Можно найти средне взвешенное значение

͞X_взвеш= 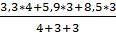= 5,64

И среднеарифметическое

͞Х_ариф = 5,69

5,69-5.64 = 0,05

σ = 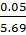* 100% = 0.88%

σ – ошибка.

– накопленное значение полигона

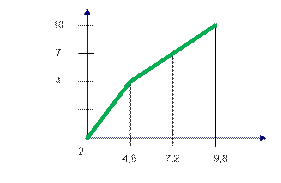
Рисунок 10

СВ в относительных величинах:

ОВ =

Число попаданий →частота попаданий (вероятность)

Дифференциальный закон распределения:

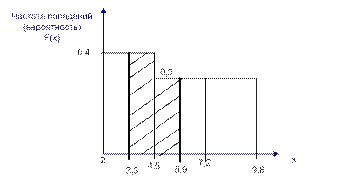
Рисунок 1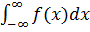1

= 1

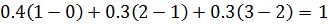
Интегральный закон распределения:

P(x≤9.8) = 1 P (x< 7.2) = 0.7

Рисунок 12

Законы распределения позволяют решать задачи, связанные с определением вероятность попадания значений случайной величины в заданный интервал.

[3.3;5.9] – заданный интервал

Дифференциальный закон:

D₀ = 2.6 - 1 –абсолютная величина

D = 1 – относительная величина

4.6 - 3.3 = 1.3 – x

Абсолютная относительная

х = 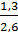= 0,5

D_n= 2.6 – 1

5.9 - 4.6 = 1.3 – y

y =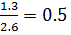

0.4 * 0.5 + 0.5 * 0.3 = 0.35 = P(3.3≤ x ≤ 5.9)

Интегральный закон распределения

F(x = 5.9) = (P ≤ 5.9)

F(x = 3.3) = (P ≤ 3.3)

F(x=5.9) - F(x = 3.3) = P(x≤5.9) - P(x≤3.3) = P(3.3≤ x ≤ 5.9)

3-й учебный вопрос

Законы распределения. Биноминальный закон

Для того, чтобы построить дифференциальный закон распределения значения гистограммы делятся на число значений исходного ряда случайной величины. В результате по оси ординат будет откладываться не число попаданий (это абсолютная величина), а частота попаданий (это относительная величина) значений случайной величины в заданные интервалы. В свою очередь, частота попаданий значений случайной величины представляет собой вероятность.

Значение вероятности попаданий значений случайной величины в интервал, определяемый нижней границей первого интервала и верхней границей последнего интервала равняется 1. Исходя из этого длительность интервалов по оси абсцисс в дифференциальном законе берутся единичными. В этом случае границы интервалов определяются числами 0; 1; 2 … и т. д.

Аналогичным образом по кумуляте строится интегральный закон распределения случайной величины. Последнее значение интегрального закона равняется 1.

Если взять дифференциальный закон распределения случайной величины f(x), то любому заданному значению x^* соответствует вероятность его появления, равная f(x^*). Если взять интегральный закон распределения случайной величины F(x), то любому заданному значению x^* соответствует вероятность F(x^*) того, что выполняется соотношение 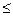x x^*.

Дифференциальный и интегральный законы распределения взаимосвязаны между собой. Так, располагая дифференциальным законам распределения f(x), по формуле (2) может быть найдены интегральный закон распределения F(x)

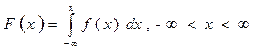
(2)

Располагая интегральным законом распределения F(x), по формуле (3) может быть найден дифференциальный закон распределения f(x)

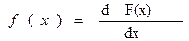
(3)

Наличие дифференциального и интегрального законов распределения случайной величины x дает возможность решения задачи, связанной с определением вероятности попадания ее значений в заданный интервал [a; b]. Если взять дифференциальный закон распределения f(x), то значение этой вероятности по формуле (4)

(4)

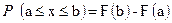Если взять интегральный закон распределения F(x), то значение этой вероятности находится по формуле (5)

5)

(

К основным числовым характеристикам случайной величины x относится: математическое ожидание M (x) или среднее 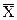; дисперсия D (x), среднеквадратичное и среднелинейное отклонение .

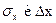Если для определения значений этих показателей использовать дифференциальный закон распределения f (x), то они могут быть найдены с помощью формул (6) – (9)

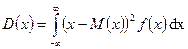
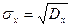
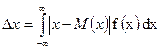
Используя формулы (6) – (9), предполагается что дифференциальный закон распределения f (x) представляет собой непрерывную функцию. Чаще этот закон является дискретным, т.е. включает в себя некоторую совокупность значений вероятности K, поставленных в соответствие K значением случайной величины. В последнем варианте мы имеем 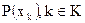, при этом .

Если берется дискретный дифференциальный закон распределения случайной величины, то выражения (6), (7) и (9) преобразуется к виду (10), (11) и (12).

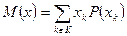
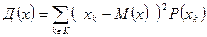
Известны формулы начальных и центральных моментов случайной величины m порядка. Они имеют вид

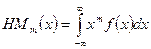
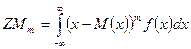
Учитывая данное обстоятельство видно, что математическое ожидание является начальным моментом 1 порядка, дисперсия – центральным моментом 2 порядка.

Если взять ряд значений случайной величины 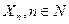, то среднее значение может быть найдено либо по формуле (15), либо по формуле (16)

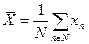
При использовании формулы (15) находится среднеарифметическое значение случайной величины Х, при использовании формулы (16) – средневзвешенное значение случайной величины Х. Значения 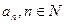представляют собой веса, поставленные в соответствие различным значениям случайной величины Х.

Формула средневзвешенной является более общей по сравнению с формулой среднеарифметической. Так, если для формулы (16) предположить справедливость соотношения 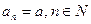, то она приводится к формуле (15).

Дисперсия и среднелинейное отклонение, если взять ряд значений случайной величины 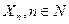, могут быть найдены по формуле (17), (18), (19), (20)

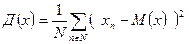
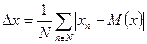
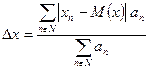
Формула (17) и (19) представляет собой формулу для определения среднеарифметического значения дисперсии D(x) и среднелинейного отклонения . Формула (18) и (20) представляет собой формулу для определения средневзвешенного значения дисперсии D(x) и среднелинейного отклонения .

Законы распределения случайной величины являются эмпирическими и теоретическими. Эмпирическим законом распределения является закон, построенный на основе опытных данных. Теоретический закон распределения случайной величины имеет определенную зависимость, выраженную соответствующей функцией.

Наиболее распространенными теоретическими законами являются:

1. Нормальный закон распределения

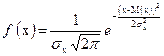
(21)

2. Равновероятный закон распределения

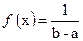
где b и a – максимальное и минимальное значение случайной величины.

Для данного закона

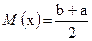
	(22)
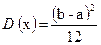
	(23)

3. Закон распределения Пуассона

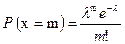
(24)

где m – целое число.

Для данного закона

(25)

4. Экспоненциальный закон распределения

(26)

Для этого закона

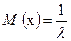
	(27)
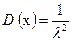
	(28)

Помимо этих законов распределения существует биноминальный закон, распределение χ² (Пирсона), распределение Стьюдента (t распределение) и распределение Фишера (или F распределение).

Предполагается, что любой эмпирический закон при увеличении числа значений случайной величины приближается к одному из известных теоретических законов распределения. По этой причине после построения эмпирического закона достаточно часто решается задача, связанная с определением соответствия его некоторому заданному теоретическому закону. Для решения данной задачи используются критерии согласия, из которых наиболее распространенным является критерий согласия Пирсона.

Суть решения указанной выше задачи с помощью критерия Пирсона сводится к следующему.

Принимается справедливость соотношений (29) и (30)

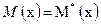
	(29)
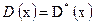
	(30)

где M(x) и M^*(x) – математическое ожидание случайной величины x для заданного теоретического и найденного эмпирического закона распределения; D(x) и D^*(x) – дисперсия случайной величины x для заданного теоретического и найденного эмпирического закона распределения.

Далее находится мера расхождения теоретического и эмпирического законов распределения u

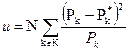
(31)

где k – число разрядов (интервалов), на которые разбивается абсцисса, являющаяся одной из осей координат при построении эмпирического закона распределения; P_k – вероятность, соответствующая середине k разряда (интервала) для теоретического закона распределения; P^*_k – вероятность, соответствующая середине k разряда (интервала) для эмпирического закона распределения.

Далее предполагается, что значение u, полученное с помощью формулы (31), является некоторым конкретным значением случайной величины U, которая, как доказал Пирсон, подчиняется закону распределения χ².

Используя данную гипотезу, находится вероятность того, что U > u. Если эта вероятность мала, то гипотеза о соответствии рассматриваемых теоретического эмпирического закона распределения отвергается, если эта вероятность велика – то эта гипотеза не отвергается. Для расчета вероятности P (U > u) используется таблица, включающая в себя значения этой вероятности, поставленные в соответствие числу степеней свободы m. Число степеней свободы m находится как разность между числом разрядов k (числом интервалов) и числом накладываемых ограничений S. В данном случае S = 2. Это обусловлено ранее принятым предположением о равенстве математического ожидания и дисперсии для рассматриваемых эмпирического и теоретического законов распределения.

Помимо числа свободы для определения значения P (U > u) используется значение найденной меры расхождения теоретического и эмпирического распределения u.

Заключение – до 5 мин.

В данной лекции рассмотрены основные понятия случайной величины, законы распределения. Биноминальный закон. Построение гистограммы

Ответить на вопросы студентов.

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Дата добавления: 2014-01-13