Введение – до 5 мин

ТЕКСТ ЛЕКЦИИ

ЛЕКЦИЯ № 3 и №4

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Кафедра ЭФ-2 «Экономические информационные системы»

УТВЕРЖДАЮ

Заведующий кафедрой ЭФ-2

_________________ Лагунова А.Д.

«____»_____________2012г.

Для студентов факультета ЭФ

специальности 080801

к.т.н. Зуев А.С., к.т.н., проф. Дмитриев Я.В.

по дисциплине «Эконометрика»

ТЕМА «Система случайных величин» ТЕМА «Случайные функции»

Обсуждена на заседании кафедры

(предметно-методической секции)

«15»мая 2012 г.

Протокол № 11

МГУПИ – 2012г.

Тема лекции: Система случайных величин. Случайные функции

Время: 4 часа (180 мин.)

ПЛАН ЛЕКЦИИ:

Введение – до 5 мин.

Основная часть (учебные вопросы) – до 170 мин.

1-й учебный вопрос

Система случайных величин. Двухмерный, трехмерный, и т.д. законы распределения, их построение и использование. Связь двухмерного с одномерными законами распределения случайных величин. – 85 мин.

2-й учебный вопрос

Случайные функции и их характерные особенности. Многомерные функции распределения при характеристике случайных функций. Стационарные и нестационарные случайные функции. Свойство эргодичности стационарных случайных функций. Ковариационная и корреляционная функция, ее построение и назначение. Прямое преобразование Лапласа и частотные характеристики функции, изменяющейся во времени. Спектральная плотность случайной функции. – 85 мин.

Заключение – до 5 мин.

Система случайных величин. Дифференциальный и интегральный закон распределения системы случайных величин. Двухмерный, трехмерный, и.т.д. законы распределения, их построение и использование. Связь двухмерного с одномерными законами распределения случайных величин. Условная плотность распределения случайных величин.

Случайные функции и их характерные особенности. Многомерные функции распределения при характеристике случайных функций. Стационарные и нестационарные случайные функции. Свойство эргодичности стационарных случайных функций. Ковариационная и корреляционная функция, ее построение и назначение. Прямое преобразование Лапласа и частотные характеристики функции, изменяющейся во времени. Спектральная плотность случайной функции.

Основная часть – до 170 мин.

1-й учебный вопрос	Система случайных величин. Двухмерный,
трехмерный, и.т.д. законы распределения, их построение и использование.
Связь двухмерного с одномерными законами распределения случайных
величин.

Возможно, когда одновременно рассматриваются не одна, а несколько случайных величины. Для них в качестве характеристики могут использоваться законы распределения.

Пусть число таких случайных величин равняется двум: X и Y. Предположим, что по каждой из этих случайных величин имеется соответствующая гистограмма. В этом случае строится гистограмма по двум случайным величинам. В ней для каждой области, определяемой определенным интервалом значений случайных величин X и Y, находится число попаданий этих случайных величин одновременно.

Далее от построенной гистограммы двух случайных величин переходим к их дифференциальному закону распределения f (x, y). Для этого по каждой случайной величине X и Y берутся интервалы единичной длительности. Далее суммируются все значения полученной гистограммы двух случайных величин X и Y. Каждое из полученных значений делится на указанную выше суммарную величину. В результате находится двумерный дифференциальный закон распределения f (x, y) системы случайных величин x и y.

Интегральный закон распределения F (x, y) случайных величин X и Y находится по формуле (32)

(32)

Располагая двумерным законом распределения f (x, y), можно найти одномерные законы распределения F (X) и F (Y). Для этого используются соотношения (33) и (34)

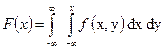
(33)

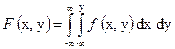
(34)

Существует связь между двумерным законом f (x, y) и одномерным законом распределения f (x) и f (y). Эта связь определена соотношениями (35) и (36)

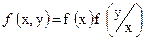
(35)

(36)

где 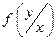и 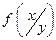- условная плотность распределения случайной величины X и Y.

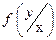характеризует собой вероятность появления значений величины Y при разных заданных значениях величины X. 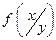характеризует собой вероятность появления значений величины X при различных заданных значениях величины Y.

Условная плотность распределения 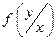и 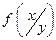может быть найдена с помощью соотношений

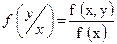
(37)

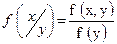
(38)

Условная плотность распределения 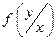и 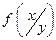используется тогда, когда случайные величины X и Y взаимосвязаны. Если же они независимы между собой, то является справедливым соотношение (39)

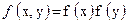
(39)

2-й учебный вопрос	Случайные функции и их характерные особенности.
Многомерные функции распределения при характеристике случайных
функций. Стационарные и нестационарные случайные функции. Свойство
эргодичности стационарных случайных функций. Ковариационная и
корреляционная функция, ее построение и назначение. Прямое
преобразование Лапласа и частотные характеристики функции,
изменяющейся во времени. Спектральная плотность случайной функции.

Случайная функция представляет собой функцию от времени, которая характеризуется некоторой совокупностью реализаций, отличающихся друг от друга. Эти реализации находятся в результате опытов, проводящихся в одинаковых условиях.

Случайная функция может являться как стационарной, так и нестационарной. Стационарная случайная функция характеризуется тем, что для различных моментов времени законы распределения соответствующих случайных величин 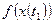, 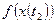и т.д. мало отличаются друг от друга. В свою очередь для нестационарной случайной функции эти законы распределения существенно отличаются между собой. Вместо законов распределения для определения того является ли случайная функция стационарной или нестационарной можно использовать математическое ожидание и дисперсию.

Стационарная случайная функция обладает свойством эргодичности. Это свойство позволяет вместо имеющейся совокупности реализаций использовать одну из них.

Если взять любую случайную функцию 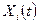, , 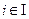где I – число ее реализаций, то для нее можно найти одномерные законы распределения 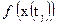, , 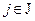где J – число рассматриваемых моментов времени. Одновременно с этим можно найти двумерные, трехмерные и т.д. законы распределения. В первом случае этот закон имеет вид 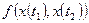, во втором случае 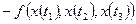, и т.д.

Законы распределения, особенно многомерные характеризуют ту или иную случайную функцию. Однако, их определение является достаточно сложной задачей.

По этой причине для анализа случайной функции используется ковариационная и корреляционная функция. При этом корреляционная функция представляет собой нормированную ковариационную функцию.

Если случайная функция является нестационарной, то ковариационная функция рассматривается по формуле (39)

(39)

где

	(40)
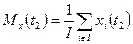
	(41)

Ковариационную функцию можно представить в виде , где τ – интервал между рассматриваемыми значениями случайной функции 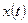. В этом случае используется формула (42), либо по формуле (43)

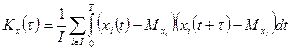
	(42)
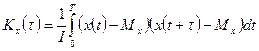
	(43)

где

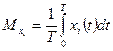
	(44)
	(45)

В формуле (42) используется некоторая совокупность реализаций случайной функции, в формуле (43) – одна из ее реализаций. В первом случае предполагается, что случайная функция является нестационарной, во втором случае – стационарной, обладающей свойством эргодичности.

В любом случае, ковариационная функция характеризует связь между значениями случайной функции, разделенными интервалами τ.

Корреляционная функция если взять формулу (42), находится с помощью соотношения (46)

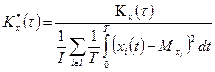
(42)

Корреляционная функция , если взять формулу (43), находится с помощью соотношения (47)

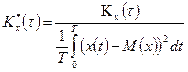
(43)

При τ = 0 корреляционная функция = 1. По I совокупности реализаций случайной функции 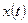можно найти ее обобщенную реализацию. Для этого считается справедливым соотношение (44)

(44)

где, 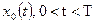- обобщенная реализация случайной функции.

Преобразуем соотношение (45). В результате получим

(45)

Будем считать справедливым соотношение (46)

(46)

В этом случае формула (45) преобразуется к виду (47)

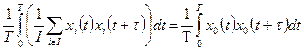
(47)

Далее можно считать справедливым соотношение (48)

(48)

Будем считать справедливым соотношение (49) и (50)

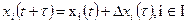
	(49)
	(50)

Подставим выражения (49) и (50)в формулу (48). В итоге получим

(51)

Будем считать справедливым соотношения

	(52)
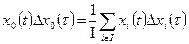
	(53)

Тогда получаем

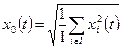
	(54)
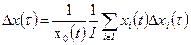
	(55)

Для анализа любой временной функции x (t), в том числе любой реализации случайной функции, можно использовать преобразование Лапласа, которое выражается соотношением (56)

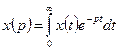
(56)

Обычно p = iω, где ω – круговая частота, равная 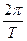(T - период), .

В этом случае выражение (56) преобразуется к виду (57)

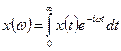
(57)

Существует формула Эйлера, которая имеет вид (58)

(58)

В этом случае выражение (57) преобразуется к виду

(59)

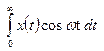и 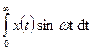представляют собой вещественную B(ω) и мнимую C(ω) часть числа X(ω).

Располагая вещественной и мнимой частями комплексного числа X(ω) можно найти значение его амплитуды и фазы. Для этого можно воспользоваться соотношениями (60) и (61)

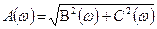
	(60)
	(61)

Располагая ковариационной функцией K(τ) можно найти её преобразование Лапласа. В этом случае амплитудная характеристика A(ω) представляет собой распределение дисперсии случайной функции x(t) по частотам. Она носит название спектральной плотности S_x(ω).

Предположим, что мы рассматриваем две случайные функции X(t) и Y(t). X(t) является входным сигналом в некоторый оператор, Y(t) – выходным сигналом.

Пусть известна спектральная плотность S_x(ω) и S_y(ω). В этом случае амплитудная частотная характеристика данного оператора определяется по формуле (62)

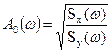
(62)

СФ имеет различные реализации отличные друг от друга, при опятах осуществляемых в одинаковых условиях.

Рисунок 13

Это функция во времени.

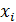(t), i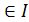, где I – число реализаций, а i – реализация.

Одномерный закон распределения:

, i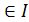– значение случайной величины.

Двумерный закон распределения:

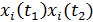, i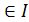

Многомерный закон распределения:

, i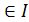

Случайные функции делятся на две группы:

1) Стационарные СФ, более устойчивые

– если во времени закон распределения в сечении не существенно меняется.

2) Нестационарные.

Эргодичность – справедлива для стационарных СФ – при исследовании СФ можно ограничится одной ее реализацией.

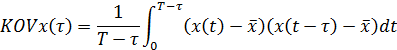
Где–– интервал взят между рассматриваемым значением СФ.

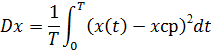
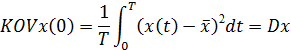
Если рассматривать совокупность реализаций

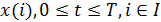
Для обобщенной реализации

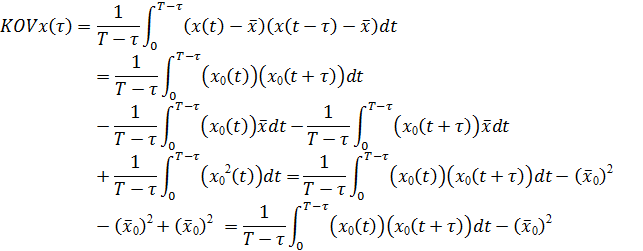
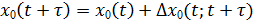
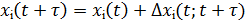
Отсюда получается

Если существуют случайные функции и 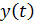, то для них ковариационная и корреляционная функции находятся по формулам:

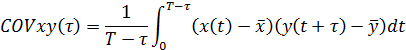
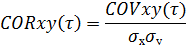
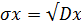
Пример Таблица 2

i
		2,2		3,1	3,3
	2,2	1,5	2,2	1,8	3,6
		3,4	1,2	2,7	2,8
	2,22	2,35	1,71	2,27	2,94
M(x)	2,07	2,37	2,13	2,53	3,23

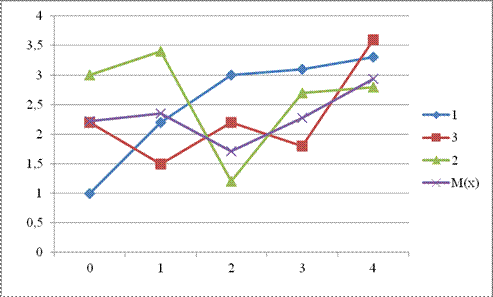
Рисунок 14

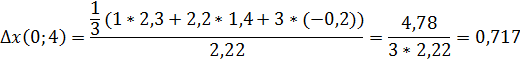
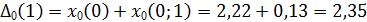
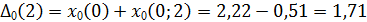
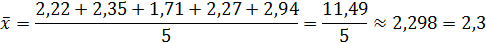
Дата добавления: 2014-01-13