Матрицы и определители. Решение систем линейных уравнений

ЛЕКЦИЯ №1.

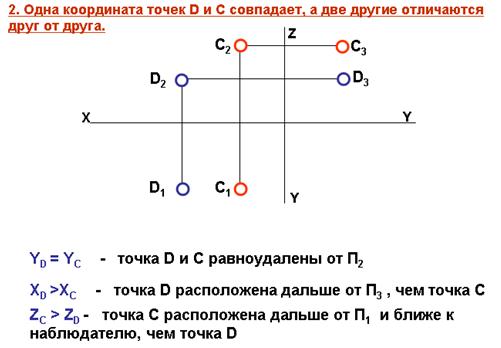
Взаимное положение точек

Даны две точки А и B принадлежащие первой четверти. Рассмотрим три случая:

Матрицей размера m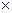n называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

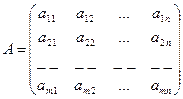
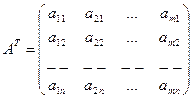- транспонированная матрица

Числа a_ij (i=1, 2, …, m; j=1, 2, …, n) называются элементами матрицы.

Коротко матрицу обозначают так:

А=(a_ij) (i=1, 2, …, m; j=1, 2, …, n)

Первый индекс – номер строки, второй – номер столбца. Если число строк матрицы равно числу столбцов (m=n), то матрица называется квадратной (порядка n):

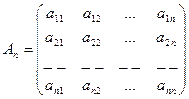
Рассмотрим систему двух линейных алгебраических уравнений:

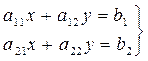
Можно составить квадратную матрицу из элементов системы:

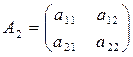
Можно составить и другие матрицы, используя столбец из свободных членов.

Например:

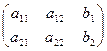- расширенная матрица системы.

Каждой квадратной матрице можно поставить в соответствие число – определитель матрицы.

Определителем второго порядка называется число, связанное с матрицей А₂ второго порядка следующим образом:

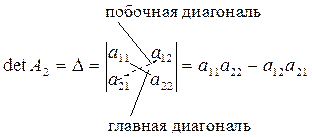
Рассмотрим систему трех уравнений:

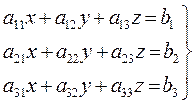
Составим матрицу из коэффициентов системы:

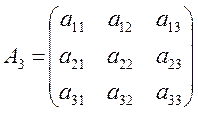(квадратная матрица 3-го порядка).

Определителем третьего порядка, соответствующим матрице А₃, называется число, определяемое равенством:

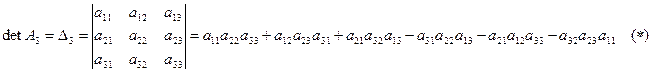
Правило треугольника:

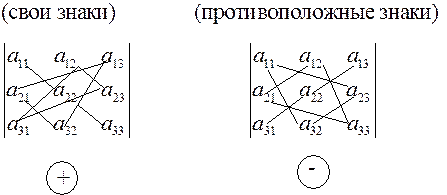
Пример.

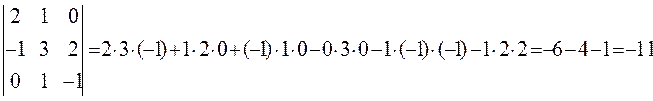
Свойства определителей.

Рассмотрим свойства, которыми обладают определители любого порядка. Для простоты будем проверять их только для определителей 2-го и 3-го порядка.

1. Если в определителе заменить все строки соответствующими столбцами, сохраняя индексы элементов, то определитель не изменится.

Доказательство. Действительно:

∆=∆^|

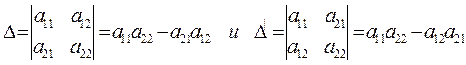
(Равноправие строк и столбцов определителя)

Поэтому свойства определителя можно формулировать только для строк.

2. Если две строки определителя поменять местами, то определитель изменит знак на противоположный.

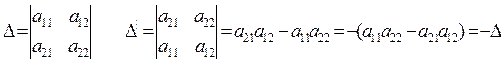
3. Если в определителе две строки совпадают, то такой определитель равен нулю.

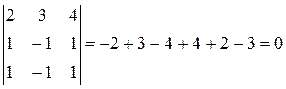
Док-во. При перестановки двух одинаковых строк определитель не изменится, а по св-ву (2) он должен изменить знак:

.

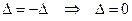Введем понятие минора и алгебраического дополнения элемента a_ij определителя ∆.

Минором M_ij элемента a_ij определителя ∆ называется определитель, полученный из данного вычеркиванием i-строки и j-го столбца.

Примеры.

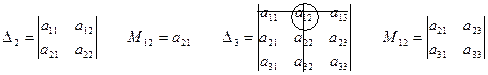
Алгебраическим дополнением А_ij элемента а_ij определителя ∆ называется минор M_ij, взятый со знаком (-1)^i+j.

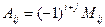
Например: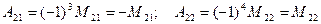

4. (О разложении определителя по элементам ряда).

Определитель равен сумме произведений всех элементов некоторого ряда на их алгебраические дополнения.

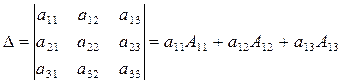(1)

Док-во.

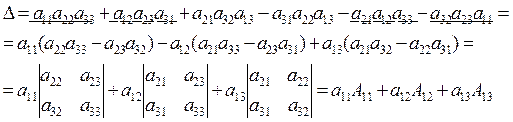
Формула (1) – разложение определителя по элементам первой строки. Аналогичные формулы можно записать для любого ряда. Это свойство очень важно, т.к. его часто используют для вычисления определителя.

5. Сумма произведений элементов любой строки определителя на алгебраические дополнения элементов другой строки равна нулю:

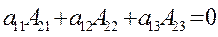(2) и т.д.

Доказательство. Действительно, левую часть равенства (2) можно представить в виде определителя с двумя одинаковыми строками, а такой определитель по свойству (3) равен нулю:

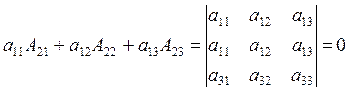(по свойству 3)

6. Общий множитель элементов любой строки можно выносить за знак определителя.

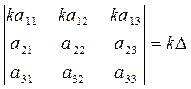
Доказательство. По предыдущему свойству:

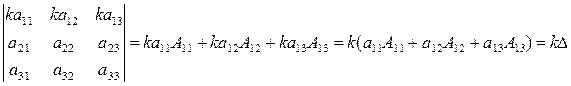
Следствие 1. Если определитель имеет две пропорциональные строки, то он равен нулю. 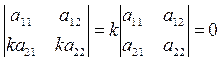(свойство 3)

Следствие 2. Если все элементы некоторой строки равны нулю, то определитель равен нулю.

Для доказательства достаточно положить k=0.

7. (об определителе, строка которого состоит из сумм)

Если элементы какой либо строки определителя являются суммой двух слагаемых, то определитель можно представить в виде суммы двух (слагаемых) определителей:

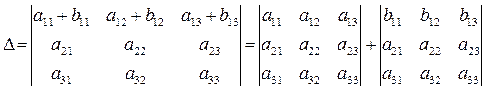
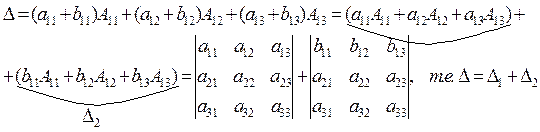
8. Если к элементам любой строки определителя прибавить элементы другой строки, умноженные на одно и то же число, то определитель не изменится.

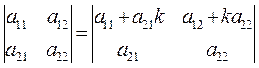
Доказательство. Преобразуем определитель в правой части:

Свойства 4, 6 и 8 часто используются при вычислении определителей. При этом, пользуясь свойством 8, стараются получить в одной строке (столбце) наибольшее количество нулей.

Пример.

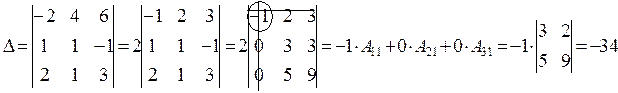
Дата добавления: 2014-01-13