
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Число сочетаний
|
|
|
|
Предположим, что по n ячейкам размещается r неразличимых между собой (в каждую ячейку можно поместить только один предмет). Тогда число различных размещений совпадает с числом различных групп по r ячеек и равно
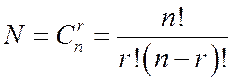 .
.
Вышеприведенная формула также определяет число подмножеств размерности r множества из n элементов, где два подмножества считаются различными, если они отличаются элементами, а порядок их следования – несущественен. Соответственно в знаменателе имеем деление на r!.
Полученная формула относится также к разбиению n различных элементов (ячеек) на две группы (группа 1 - пустые ячейки и группа 2 - занятые ячейки).
Результат разбиения можно представить в виде вектора размерности n, содержащего r единиц (признак незанятости ячейки) и (n-r) двоек (признак занятости ячейки). Два разбиения различны, если различны соответствующие им вектора.
Рассмотрим общий случай разбиения n различных элементов на k групп, причем в группе с номером i число элементов равно ni и 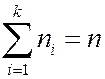 . Результат разбиения вновь можно представить в виде вектора размерности n, содержащего n1 единиц, n2 двоек, …, nk чисел k. Два разбиения различны, если различны соответствующие им вектора. Число различных разбиений дается формулой
. Результат разбиения вновь можно представить в виде вектора размерности n, содержащего n1 единиц, n2 двоек, …, nk чисел k. Два разбиения различны, если различны соответствующие им вектора. Число различных разбиений дается формулой
 .
.
Пример 1: N различных шаров случайно размещаются по М ящикам, М>N.
Найти вероятность, что все шары попадут в разные ящики.
Решение.
Число способов размещения N шаров по М ящикам равно МN.
Число способов размещения N шаров по М ящикам, когда в каждый ящик попадает по одному шару равно
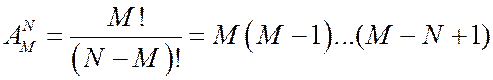 .
.
Ответ: 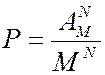
Пример 2: При игре в бридж между 4-мя игроками распределяются 52 карты (по 13 каждому). Найти вероятность, что каждому игроку достанется по тузу.
Решение.
Число разбиений 52 карт на 4 группы по 13 карт дается формулой
 , где n=52, n1= n2= n3=n4=13,
, где n=52, n1= n2= n3=n4=13, 
Найдем вероятность, что каждому игроку достанется по тузу.
Четыре туза распределяются между четырьмя игроками 4! способами. Оставшиеся 48 карт распределяются между четырьмя игроками числом способов, равных число разбиений 48 карт на 4 группы по 12 карт;  . Следовательно, искомая вероятность равна
. Следовательно, искомая вероятность равна
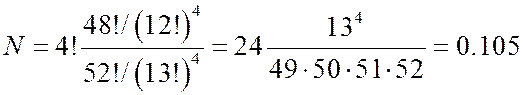 .
.
Пример 3: (гипергеометрическое распределение вероятностей).
Существует большой класс задач ТВ, которые можно интерпретировать в рамках так называемой урновой схемы: событие, вероятность которого надо вычислить, можно трактовать как выбор шаров различной расцветки из урны. Простейшая из таких схем состоит в следующем. Из урны, содержащей М черных и N-M белых шаров, случайно вынимается n шаров. Какова вероятность того, что выборка содержит m черных шаров?
Решение.
В этом эксперименте пр-во элементарных событий состоит из 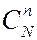 исходов. Решение задачи сводится к подсчету числа выборок из n шаров, которые содержат m черных и n-m белых шаров.
исходов. Решение задачи сводится к подсчету числа выборок из n шаров, которые содержат m черных и n-m белых шаров.
Очевидно что,  .
.
Правая часть неравенства означает, что число черных шаров m должно быть меньше объема выборки n и числа M черных шаров.
Левая часть неравенства означает, что если объем выборки n превышает число белых шаров N-M, то число черных шаров не может быть меньше, чем n-(N-M) = (размер выборки – число белых шаров).
Число способов выбора из М черных шаров m шаров равно  . Число способов выбора из N-M белых шаров n-m шаров равно
. Число способов выбора из N-M белых шаров n-m шаров равно 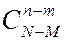 .
.
Следовательно общее число исходов, соответствующее событию А – «выборка содержит m черных шаров» равно 
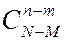 , и искомая вероятность
, и искомая вероятность
Р(А)=
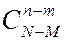 /
/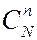 .
.
Пример 4: (Задача про рыб).
Из озера вылавливается 1000 рыб. Каждая из рыб метится красной меткой и отпускается в озеро. При следующем улове среди 1000 рыб оказалось 100 меченых. Какие выводы можно сделать относительно числа рыб?
Решение.
Пусть n – (неизвестное) число рыб в озере, n1 -число меченых рыб (n1 =1000), r – число рыб, пойманных при втором улове (r =1000), k - число меченых рыб, пойманных при втором улове (k =100).
Вероятность поймать k меченых рыб есть
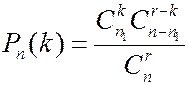 .
.
Для оценки числа рыб n предлагается найти n из условия максимума вероятности 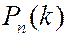 , то есть в предположении, что при втором улове реализовалось наиболее вероятное событие. Основной довод в пользу такой оценки числа рыб состоит в простом житейском наблюдении: если происходит какое-либо событие, то это событие должно иметь наибольшую вероятность среди всех остальных исходов.
, то есть в предположении, что при втором улове реализовалось наиболее вероятное событие. Основной довод в пользу такой оценки числа рыб состоит в простом житейском наблюдении: если происходит какое-либо событие, то это событие должно иметь наибольшую вероятность среди всех остальных исходов.
Для определения максимума вероятности 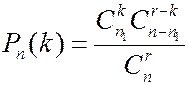 по переменной n, рассмотрим
по переменной n, рассмотрим
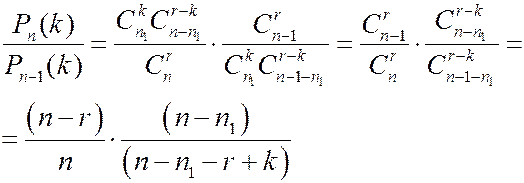
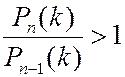 при
при 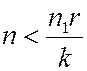 и
и 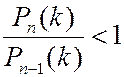 при
при  .Это значит, что при возрастании n вероятности
.Это значит, что при возрастании n вероятности 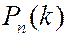 сначала возрастают, а затем убывают. Максимум достигается, когда n есть максимальное целое число, не большее чем
сначала возрастают, а затем убывают. Максимум достигается, когда n есть максимальное целое число, не большее чем 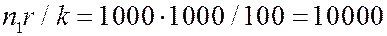 .
.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 535; Нарушение авторских прав?; Мы поможем в написании вашей работы!