Выбор без возвращения

Определение 8. Перестановками называются комбинации, состоящие из одних и тех же 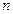различных элементов и отличающиеся только порядком их расположения.

Представим на примере распределения 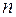элементов по 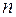ячейкам. В первую располагаем любой из 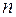элементов (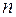способами), вторую ячейку можно заполнить 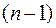способами, третью - 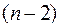и т.д. Отсюда число способов заполнения (число всех возможных перестановок) равно

(2)

Определение 9. Размещениями называются комбинации, составленные из 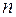различных элементов по 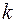элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений из 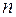различных элементов по 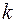элементов равно

(3)

Определение 10. Сочетаниями называются комбинации, составленные из элементов 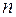различных элементов по 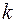элементов, которые отличаются хотя бы одним элементом. Число всех возможных сочетаний из 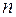различных элементов по 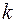элементов равно

(4)

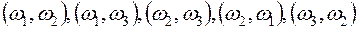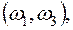
Пусть, например, дано множество . Размещениями из трех элементов этого множества по два являются ; сочетаниями: 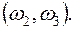Два сочетания отличаются друг от друга хотя бы одним элементом, а размещения отличаются либо самими элементами, либо порядком их следования.

Пример 10: Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? А если выбрать 1 красную гвоздику и 2 розовых?

Решение: Так как порядок выбора не имеет значения, то выбрать 3 цветка из вазы, в которой стоят 14 гвоздик, можно Красную гвоздику можно выбрать 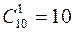способами. Выбрать две розовые гвоздики из 4-ех можно способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить по правилу умножения 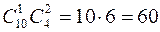способами.

Дата добавления: 2014-01-13