Системы координат, применяемые в геодезии

Широкое применение приемников спутниковых навигационных систем привело к тому, что наибольшее распространение в практике геодезии в нашей стране получили три пространственные геодезические системы координат. Во-первых, это пространственная прямоугольная система координат. Это геоцентрическая экваториальная система координат, ось Z которой направ­лена на северный полюс Земли, а ось Х — в точку Гринвича G пересечения гринвичского меридиана с эквато­ром (рис. 1.3). Полученная система координат (OXYZ) участвует в су­точном вращении Земли, оставаясь неподвижной относительно точек земной поверхности и потому удобна для определения положения объектов земной поверхности.

Положение точек земной по­верхности относительно земного эллипсоида определяется в системе пространственных эллипсоидальных координат геодезической широ­той В, долготой L и высотой Н (см. рис. 1.3).

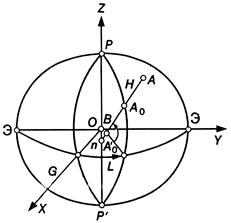
Рис. 1.3. Связь прямоугольных и эллипсоидальных координат

Геодезической широтой точки А называют острый угол В, образованный нормалью к поверхности эллипсоида в некоторой точке и плоскостью экватора ЭGЭ. Геодезической долготой точки А называют двугранный угол, образованный плоскостью начального PGP^’ и геодезического меридиана данной точки. Широты точек северного полушария называют северными и обозначают со знаком «+», соответственно южные широты сопровождают знаком «-». Точки, расположенные восточнее начального меридиана, имеют восточные долготы, западнее — западные. В отечественной геодезической литературе долготы принято отсчитывать от начального меридиана против хода часовой стрелки от 0 до 360^о. Отрезок нормали А_оА называют геодезической высотой Н.

Высота геоида над эллипсоидом отсчитывается по нормали и может иметь как положительный, так и отрицательный знаки. Отрезок А_оп называ­ют радиусом кривизны нормального сечения и обозначают через N. Отрезок

A’_on = е²N, где е² = α (2 - α), есть квадрат эксцентриситета меридианного эллипса.

Из рис. 1.3 следует, что пространственные прямоугольные координаты связаны с эллипсоидальными следующей группой формул

X=(N+H)cosBcosL,

Y=(N+H)cosBsinL, (1.1)

Z=(b²N/a² + H)sinB,

где N= a²/(a²cos²B + b²sin²B)^1/2.

Обратным преобразованием формул (1.1) можно получить формулы вычисления эллипсоидальных координат по прямоугольным следующего вида

B= arctg(Z + e^’2 b sin²θ)/(p – e²a cos²θ);

L= arctg(Y/X); (1.2)

H= p/cosB – N,

где е и е^’ -- первый и второй эксцентриситеты земного эллипсоида,

е²=(а² – b²)/ a²; e^’2=(a² – b²)/ b²,

где р и θ – вспомогательные величины, определяемые формулами

p=(X² + Y²)^1/2, θ= arctg(Za)/(pb).

Прямоугольные и эллипсоидальные пространственные координаты широко используют при уравнивании государственных геодезических сетей, решении задач высшей геодезии, в морской и воздушной навигации. При решении задач инженерной геодезии от них переходят к системе плоских прямоугольных координат в проекции Гаусса-Крюгера. В этом случае эллипсоид вписывают в поперечный цилиндр, касающийся поверхности цилиндра по осевому меридиану зоны. С целью уменьшения величин искажения при проектировании зоны из центра эллипса на боковую поверх­ность цилиндра проектируют точки поверхности эллипсоида и затем по­верхность цилиндра разворачивают в плоскость. При таком проектировании осевой меридиан зоны и экватор отображаются прямыми, которые при­нимаются за ось х и у соответственно (рис. 1.4).

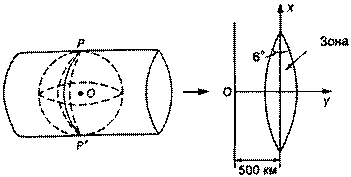
Рис. 1.4. Конформная поперечно-цилиндрическая проекция Гаусса-Крюгера

Проекция Гаусса является основной в нашей стране как для обработки геодезических координат, так и для построения топографически карт. К ее достоинству относятся: со­хранение подобия в бесконечно малых частях, т.е. конформность (равноугольность) и сохранение масштаба по оси х. Чтобы уменьшить величины искажений, ширину зоны ограничивают величиной 6° или 3° по долготе. Таким образом, в каждой зоне вводится своя система прямоугольных координат. При построении топографических карт применяют шести­градусные зоны. В нашей стране координаты х — положительные. Чтобы не применять отрицательных координат у, начало координат смещают на 500 км к западу. При оцифровке километровой координатной сетки перед координатой у ставят номер зоны. Поэтому в записи у = 4311 км первая цифра — 4 означает номер зоны, а 311 — расстояние километровой линии от смещенного меридиана зоны. Для перехода от эллипсоидальных координат к прямоугольным координатам системы Гаусса-Крюгера х и у, последние пред­ставляют в виде некоторых эллиптических функций: х =f(В,L); у=f(В,L). Для практического использования формулы дифференцируют, разлагают в ряд с необходимой степенью точности, после чего получают тот или иной вид фор­мул, удобный для вычислений. Так при работе в одной шестиградусной зоне достаточно эффективными можно считать формулы

X=S+(L²r sin B)/2 + (L²r cos²B sin B)(5 – tg²B)/24

Y= Lr + (L³r cos²B(1 – tg²B))/ 6, (1.3)

где В – геодезическая широта точки в радианах; L – отклонение от осевого меридиана зоны в радианах,

S= 6 367 558,5 B – 16 036,5 sin 2B + 16,8 sin 4B;

r= a cos B/(1 – e₂ sin B sin L)^1/2 – радиус кривизны параллели; е₂=0,00669343.

Искажения длин линий ∆S в проекции Гаусса-Крюгера возрастают по мере удаления от оси х в соответствии с формулой ∆ S =y_mS/2R, где y_m = (y₁ + y₂)/ 2 и R — средний радиус кривизны.

Для решения обратной задачи можно использовать экономичный принцип сжимающих отображений в соответствии с формулами

L=r(y – (L²r cos² B(1- tg²B)))/6,

B=(x+16036,5sin2B – 16,8sin4B – (Lr sinB)/2 –(L⁴r cos²B sin B) ×

× (5 – tg²B)/24)/ 6367558,5.

Итерационный процесс вычисления долготы L и широты B точки сходится достаточно быстро.

Кроме перечисленных геодезических, в практике геодезии широко исполь­зуют две сферические системы координат: астрономическую и географичес­кую. Координатами в них являются широта и долгота точки сферы. Астрономическая широта (φ — угол, образованный отвесной линией в данной точке и плоскостью, перпендикулярной оси вращения Земли. Астрономичес­кая долгота λ — двугранный угол, составленный плоскостями начального ме­ридиана и меридиана данной точки. Достоинство астрономических координат заключается в автономности их определения для каждой точки. Расхождения между эллипсоидальными и астрономическими широтами и долготами обусловлено, как уже было отмечено ранее, уклонением отвесной линии от нормали к поверхности референц-эллипсоида. Уклонения отвеса даже в горных районах не превышают 30 — 40", поэтому при составлении карт ими чаще всего пренебрегают и отождествляют обе системы координат, называя общую систему географической.

Дата добавления: 2014-01-13