
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория подобия
|
|
|
|
Физическое моделирование
Физическое моделирование проводится на основе экспериментального исследования материальных моделей объекта. При этом возникают три проблемы: какую модель использовать (форма, размер, модельные среды), какие характеристики измерять и как перенести результаты исследований с модели на объект. Эти проблемы разрешаются с помощью теории подобия, являющейся теоретической основой физического моделирования.
Подобие в широком смысле - это возможность распространения результатов эксперимента с модели на оригинал. В узком смысле подобие - это тождественность описания полей соответствующих величин модели и оригинала в обобщенных переменных или по-другому - постоянство отношения сходственных величин модели и оригинала. В дальнейшем термин подобие будет использоваться в узком смысле, отвечающем более жестким требованиям. Теория подобия на основе исчерпывающего математического описания процессов переноса определяет условия, при которых соблюдается подобие модели и оригинала. Это позволяет вместо математического решения системы дифференциальных уравнений совместно с условиями однозначности получать результаты интегрального решения экспериментально, исследуя модель.
Подобные объекты описываются одной системой дифференциальных уравнений и имеют подобные условия однозначности. Подобие условий однозначности включает в себя геометрическое подобие, временное подобие, подобие физических величин, подобие начальных и граничных условий.
Геометрическое подобие - постоянство отношения всех сходственных линейных размеров модели и оригинала.
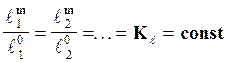
где 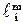 и
и 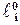 - сходственные линейные размеры модели и объекта (длина, диаметр и т.д.),
- сходственные линейные размеры модели и объекта (длина, диаметр и т.д.), 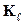 - константа геометрического подобия.
- константа геометрического подобия.
Сходственные точки - точки, удовлетворяющие условию геометрического подобия.
Временное подобие (гомохронность) - постоянство отношения сходственных интервалов времени модели и оригинала.
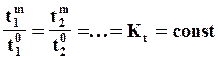
Если константа временного подобия Kt=1, то такой частный случай гомохромности называют синхронностью, при этом сходственные интервалы времени модели и оригинала совпадают.
Подобие физических величин - постоянство отношения физических величин для модели и оригинала в сходственных точках в сходственные моменты времени
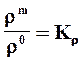 ;
; 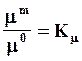 ;
; 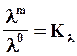
В общем случае Kr¹Km ¹ Kl. Подобие модели и объекта предполагает подобие полей физических величин.
Wm/W0=Kw - гидродинамическое подобие (подобие полей скорости)
Tm/T0=Kт – тепловое подобие (подобие полей температуры)
Cim/Ci0=Kс -концентрационное подобие (подобие полей концентраций)
Подобие начальных условий - подобие полей всех физических величин в начальный момент времени.
Подобие граничных условий - постоянство отношения соответствующих величин на границах модели и оригинала.
Константы подобия - (отношения одноименных величин модели и оригинала) постоянны для различных сходственных точек подобных систем, но изменяются при переходе от одной модели к другой.
Инварианты подобия - безразмерные отношения величин, характеризующих модель или оригинал. Их значения могут изменяться в пространстве и во времени, но в случае подобия одинаковы для модели и оригинала в сходственных точках в сходственные моменты времени и не меняются при переходе от одной подобной модели к другой.
Инварианты подобия еще называют обобщенными, относительными или безразмерными переменными, а также критериями подобия, т.к. они служат признаком, по которому можно судить о подобии модели и оригинала. Инварианты (критерии) подобия подразделяются по различным признакам в зависимости от вида величин, их составляющих на: 1. симплексы и комплексы подобия; 2. определяющие и определяемые критерии; 3. независимые, зависимые и постоянные обобщенные переменные.
Симплексы подобия - инварианты подобия, представляющие отношения однородных величин.
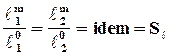
Комплексы подобия - инварианты подобия, представляющие отношение разнородных величин.
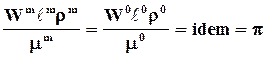
Определяющие критерии подобия - составлены из величин, входящих в условия однозначности.
Определяемые критерии подобия - содержащие величины, требующиеся определить в ходе решения задачи.
Независимые обобщенные переменные - содержащие текущие значения пространственных координат и времени.
Зависимые обобщенные переменные - содержащие величины, меняющиеся в зависимости от независимых.
Постоянные обобщенные переменные - постоянные для группы подобных объектов (определяющие критерии подобия).
Если объект характеризуется несколькими значениями однородных величин, например, несколькими линейными размерами (длина, ширина, высота), то во всех комплексах подобия используется, как правило, только одна из них, называемая характерной. Характерная величина - наиболее удобная, показательная для характеристики данного объекта применительно к рассматриваемой задаче.
Наиболее простой алгоритм получения критериев подобия заключается в следующем: дифференциальное уравнение приводится к безразмерному виду делением всех членов на один из них; все приращения заменяют на абсолютные значения величин; полученные комплексы, количество которых на единицу меньше числа первоначальных членов уравнения, являются критериями подобия.
В качестве примера рассмотрим получение критерия Ньютона из одноименного уравнения
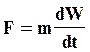 ;
; 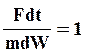 ;
; 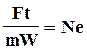 (73)
(73)
Рассмотрим без доказательства три теоремы подобия.
1.Подобные объекты характеризуются численно равными критериями подобия (Ньютон, Бертран).
2.Решение дифференциального уравнения (системы уравнений), описывающего объект, может быть представлено в виде зависимости между критериями подобия (Бэкингем, Федерман, Афанасьева-Эренфест).
3.Объекты подобны, если они описываются одной системой дифференциальных уравнений, имеют подобные условия однозначности и их определяющие критерии численно равны (Кирпичев, Гухман). Они могут быть дополнены p -теоремой Бэкингема, являющейся основой метода анализа размерностей: любую зависимость между N величинами, среди которых n обладают независимыми размерностями, можно представить уравнением, связывающим N - n = Nk безразмерных комплексов, составленных из этих величин (при наличии подобия Nk критериев подобия). При этом, если Nn величин имеют неодинаковую размерность, то Ns = N - Nn критериев подобия могут являться симплексами подобия. Группа величин обладает независимыми размерностями, если размерность каждой из них не может быть представлена в виде степенного комплекса размерностей остальных.
Первая и третья теоремы формулируют необходимые и достаточные условия подобия модели и оригинала, а вторая, совместно с p - теоремой позволяет выделить минимальное число обобщенных переменных, с помощью которых может быть выражено интегральное решение. Такое решение, представляющее зависимость между критериями подобия, носит название критериального уравнения. Следует иметь в виду, что комбинация критериев также является критерием подобия. Конкретный вид уравнения получается обобщением результатов исследования на модели. Критерий, который в соответствии с поставленной задачей содержит искомую величину, называется определяемым, а остальные - определяющими. Равенство определяющих критериев модели и оригинала приводит к равенству определяемых критериев. Обычно критериальные уравнения представляют степенную зависимость
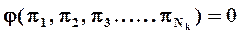 (74)
(74)
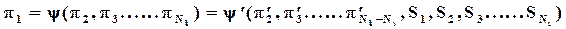 (75)
(75)
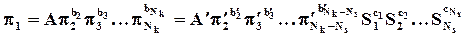 (76)
(76)
где p1 - определяемый критерий, p2..... pNk - определяющие критерии, A, bi,ci - экспериментально найденные коэффициенты, Si - симплексы подобия.
Если какой - либо из определяющих критериев, слабо влияет на определяемый (показатель степени близок к нулю), то его можно исключить из уравнения. В этом случае говорят об автомодельности процесса по отношению к данному критерию. Зачастую не удается соблюсти равенство всех критериев модели и объекта, в этом случае добиваются совпадения критериев, наиболее значительно влияющих на процесс, осуществляя приближенное моделирование.
Таким образом, теория подобия позволяет обобщать результаты эксперимента и распространять их на широкий класс подобных явлений.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 5069; Нарушение авторских прав?; Мы поможем в написании вашей работы!