Цифра Код с избытком 3 Код 4221

0 0011 0000

1 0100 0001

2 0101 0010

3 0110 0011

4 0111 1000

5 1000 0111

6 1001 1100

7 1010 1101

8 1011 1110

9 1100 1111

Эти коды обладают важным свойством: для того, чтобы для какой-либо цифры получить ее дополнение до 9, достаточно взять ее обратный код. Это позволяет упростить десятичную арифметику точно так же, как применение дополнительного кода упрощает двоичную арифметику. Вместо вычитания какого-либо числа достаточно произвести сложение с числом, которое представляет собой дополнение до 9 исходного числа плюс 1.

Пример: 27-15= 27

+85 (дополнение до 9 числа 15 = 84, затем прибавили 1)

Код Грея используется в механических шифраторах угла поворота вала. При переходе из любого его состояния к следующему изменяется лишь один разряд. Это позволяет предотвратить ошибки, так как в данном случае при переходе между двумя соседними значениями все разряды не могут измениться одновременно.

(0000) (1100)

(0001) (1101)

(0011) (1111)

(0010) (1110)

(0110) (1010)

(0111) (1011)

(0101) (1001)

(0100) (1000)

Представление чисел в соответствии с формулой

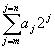
называется представлением чисел с фиксированной точкой. Такой способ дает возможность при фиксированных значениях m и n представить числа в диапазоне от 2^m до 2ⁿ⁺¹-1. Например при m=0 и n=7, т.е. с помощью 8-разрядного двоичного кода можно представить числа в диапазоне от 0 до 255, а в случае необходимости представления отрицательных чисел, от -127 до +127. Такой диапазон представления чисел в ряде случаев оказывается недопустимо маленьким, что влечет за собой усложнение алгоритмов обработки данных с большим диапазоном изменения.

Для представления чисел в большом диапазоне изменения величин применяется т.н. формат с плавающей точкой. В этом формате число представляется в виде

,

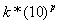где k называется мантиссой, а p - порядком числа. Значения k и p представляются в свою очередь в обычном формате с фиксированной точкой. Нетрудно видеть, что при использовании того же 8-разрядного двоичного кода для представления мантиссы и порядка, с помощью формата с плавающей точкой можно представить числа в диапазоне от (10)^-127 до (10)¹²⁸. Налицо значительное увеличение диапазона изменения чисел, однако для их хранения необходимо уже не один, а два байта (для мантиссы и порядка).

Как и для формата с фиксированной точкой, при представлении чисел с плавающей точкой используются специальные алгоритмы арифметических операций над такими числами.

Шестнадцатеричная система счисления применяется для сокращения записи двоичных чисел. Каждые соседние 4 разряда в двоичной записи числа представляются в виде одного 16-ричного разряда. Для представления чисел от 10 до 15 применяются буквы от A до F.

Пример:

Шестнадцатеричное представление наилучшим образом соответствует байтовой структуре ЭВМ (1 байт = 8 бит). Один байт представляется в виде 2 шестнадцатеричных цифр. Чтобы преобразовать число из двоичной кода в шестнадцатеричный необходимо разбить код числа на группы из 4 бит начиная с младшего разряда и представить каждую группу в виде одной шестнадцатеричной цифры. Чтобы преобразовать число из шестнадцатеричного кода в двоичный необходимо последовательно записать каждую шестнадцатеричную цифру в виде 4 двоичных разрядов.

Дата добавления: 2014-01-13