Поиск в строке. Алгоритм Боуера и Мура

...........

BEGIN

VAR

i, j, k, k0, M, N: INTEGER;

Ch: CHAR;

p: ARRAY [1.. Mmax] OF CHAR; { образ }

s: ARRAY [1.. Nmax] OF CHAR; { строка }

d: ARRAY [1.. Mmax] OF INTEGER;

{ ввод элементов (символов) в массивы p и s }

j:= 1; k:=0; d[1]:=0; { предтрансляция }

WHILE j < M DO BEGIN

WHILE (k>0) AND (p[j] <> p[k]) DO k:=d[k];

j:=j+1; k:=k+1;

IF p[j]=p[k] THEN d[j]:=d[k] ELSE d[j]:=k;

END;

i:=1; j:= 1; } { поиск КМП }

WHILE (j <= M) AND (i <= N) DO BEGIN

WHILE (j>0) AND (s[i] <> p[j]) DO j:=d[j];

j:=j+1; i:=i+1;

END;

IF j=M+1 THEN ….. { поиск удачный };

……

Анализ КМП-поиска. Точный анализ КМП-поиска, как и сам его алгоритм, весьма сложен, Его изобретатели доказывают, что требуется порядка M+N сравнений символов, что значительно лучше, чем M*N сравнений из прямого поиска. Они так же отмечают то приятное свойство, что указатель сканирования i никогда не возвращается назад, в то время как при прямом поиске после несовпадения просмотр всегда начинается с первого символа об­раза и поэтому может включать символы, которые ранее уже просматривались. Это может привести к неприятным затруднениям, если строка читается из вторичной памяти, ведь в этом случае возврат об­ходится дорого. Даже при буферизованном вводе мо­жет встретиться столь большой образ, что возврат превысит емкость буфера.

Примечание:

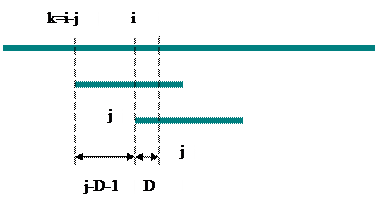
В этом алгоритме вообще отсутствует необходимость сравнения образа с самого его начала в случае если до этого было частичное совпадение образа и строки. Фактически выигрыш достигается за счет двух составляющих:

1. за счет сдвига;

2. за счет тех D символов образа, которые не сравниваются с соответствующими символами строки

Остроумная схема КМП-поиска дает подлинный выигрыш только тогда, когда неудаче предшество­вало некоторое число совпадений. Лишь в этом случае образ сдвигается более чем на единицу. К несчастью, это скорее исключение, чем правило: совпадения встречаются значительно реже, чем несовпадения. Поэтому выигрыш от использования КМП-стратегии в большинстве случаев поиска в обычных текстах весьма незначителен. Метод же, о котором сейчас пойдет речь, в действительности не только улучшает обработку самого плохого случая, но дает выигрыш в промежуточных ситуациях. Его предложили Р.Боуер и Д.Мур приблизительно в 1975 г; мы бу­дем называть его БМ-поиском. Вначале мы дадим упрощенную версию этого алгоритма, а затем перей­дем к той, которую приводят Боуер и Мур.

БМ-поиск основывается на необычном соображе­нии—сравнение символов начинается с конца об­раза, а не с начала. Как и в случае КМП-поиска, образ перед фактическим поиском трансформируется в некоторую таблицу. Пусть для каждого символа х из алфавита d_x —расстояние от самого правого в об­разе вхождения х до его конца. Представим себе, что обнаружено расхождение между образом и строкой. В этом случае образ сразу же можно сдвинуть вправо на d_p позиций, т. е. на число позиций, скорее всего большее единицы. Если s_i (s_i -символ соответствующий позиции p_m) в образе вооб­ще не встречается, то сдвиг становится даже больше, а именно сдвигать можно на длину всего образа. Вот пример, иллюстрирующий этот процесс:

и

в

а

н

о

в

и

в

а

н

и

в

а

н

ы

ч

и

в

а

н

ы

и

в

а

н

ы

и

в

а

н

ы

и

в

а

н

ы

Поскольку сравнение отдельных символов теперь проходит справа налево, то более удобно использо­вать такие слегка модифицированные версии преди­катов Р и Q:

P(i, j) = A k: j ≤ k ≤ M: s_i-j+k=p_k (1.53)

Q(i) = A k: 1 ≤ k < i: ~ P(i,1)

Эти предикаты используются при описании БМ-алгоритма, и с их помощью формулируются инвариант­ные условия.

i:=M; j:=M; (1.54)

WHILE (j > 0) AND (i <= N) DO BEGIN

(* Q(i-M) *)

k:=i; j:=M;

WHILE (j >= 1) AND (s[ k ] = p[ j ]) DO BEGIN

(* P(k-j,j) & (k-j = i-M) *)

k:=k-1; j:=j-1;

END;

i:= i + d[ s[i] ]

END;

Индексы удовлетворяют условиям 0 ≤ i, k ≤ N и 0 ≤ j ≤ M. Поэтому из окончания при j = 0 вме­сте с P(k-j,j) следует P(k,0), т. е. совпадение в позиции k. При окончании с j > 0 небходимо, чтобы j=N, следовательно, из Q(i-М) имплицируется Q(N—М), сигнализирующее, что совпадения не су­ществует. Конечно, мы продолжаем убеждаться, что Q(i—М) и P(k—j,j) действительно инварианты двух циклов. В начале повторений они, естественно, удовлетворяются, поскольку Q(0) и Р(х,М) всегда истинны.

d: array [#0..#200] of byte;

{ предтрансляция }

FOR c:=#0 TO #200 DO d[ c ]:=M;

FOR i:=1 TO M-1 DO d[ y[i] ]:=M-i;

{ поиск методом БМ }

i:=M; j:=M;

WHILE (j>0) AND (i<=N) DO BEGIN

j:=M; k:=i;

WHILE (j>0) AND (s[k]=y[j]) DO BEGIN

j:=j-1; k:=k-1;

END;

i:=i+d[ s[i] ]

END;

Программа 1.3. Поиск упрощенным методом БМ.

Анализ поиска по Боуеру и Муру. В первоначаль­ной публикации алгоритма приводится деталь­ный анализ его производительности. Его замечательное свойство в том, что почти всегда, кроме спе­циально построенных примеров, он требует значи­тельно меньше N сравнений. В самых же благоприят­ных обстоятельствах, когда последний символ образа всегда попадает на несовпадающий символ текста, число сравнений равно N/M.

Авторы приводят и несколько соображений по по­воду дальнейших усовершенствований алгоритма. Одно из них— объединить приведенную только что стратегию, обеспечивающую большие сдвиги в слу­чае несовпадения, со стратегией Кнута, Морриса и Пратта, допускающей «ощутимые» сдвиги при обнару­жении совпадения (частичного). Такой метод требует двух таблиц, получаемых при предтрансляции: d1 — только что упомянутая таблица, а d2 —таблица, со­ответствующая КМП-алгоритму. Из двух сдвигов выбирается больший, причем и тот и другой «гово­рят», что никакой меньший сдвиг не может привести к совпадению. От дальнейшего обсуждения этого предмета мы воздержимся, поскольку дополнитель­ное усложнение формирования таблиц и самого по­иска, кажется, не оправдывает видимого выигрыша в производительности. Фактические дополнительные расходы будут высокими и неизвестно, приведут ли все эти ухищрения к выигрышу или проигрышу.

Дата добавления: 2014-01-13