Лекция №14. Современные ПЭМ с высоким разрешением порядка 0,15 -0,2 нм позволяют при подходящих условиях получить прямое изображение решетки

Современные ПЭМ с высоким разрешением порядка 0,15 -0,2 нм позволяют при подходящих условиях получить прямое изображение решетки. Для использования возможностей современных микроскопов высокого разрешения (ПЭМ ВР) необходимо подробнее рассмотреть формирование изображения в оптической системе – объективной линзе. Будем рассматривать объект, расположенный несколько дальше передней фокальной плоскости объектива, как чисто фазовый. Для него функция прохождения имеет вид:

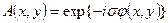- функция, описвающая фазовый объект.

Здесь 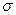-константа взаимодействия- коэффициент преломления;

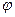(x,y)-изменение фазы в точках x, y.

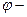трансмиссионная функция объекта..

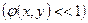Функция 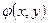представляет собой прекцию распределения электрического потенциала на плоскость (x,y). Очевидно

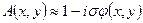(9)

В фокальной плоскости объективной линзы формируется дифракционное изображение Фурье преобразование функции объекта.:

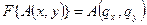. (10)

Здесь 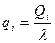-координаты в пространстве векторов рассеяния Q_i. Подставив (10) в (9) получим:

,

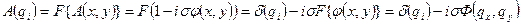где Ф(q_i)-преобразование Фурье фазовой функции .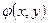

Любая оптическая система вносит искажения при формировании изображения, называемые аберециями.Аберрации искажают как фазу так и амплитуду функции А(q_i). Чтобы это учесть следует записать дифракционное изображение в виде:

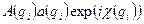, (11)

где 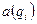- апертурная ошибка – функция, описывающая на краях диафрагмы;

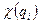- ошибка, вносимая оптической системой в фазу волны.

Разрешающая способность микроскопа определяется компромиссом между выбором большей апертуры и ростом в связи с этим аберраций. В плоскости изображения объекта путем обратного преобразования Фурье получим:

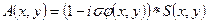, (12)

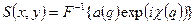- передаточная функция оптической системы (ПФ).

Если система идеальная то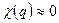и передаточная функци определяется только величиной апертуры и имеет вид:

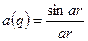, (13)

r-координата, так как апертура круглая,

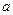-числовая апертура.

Теперь распределение интенсивности на изображении фазового объекта 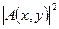можно записать в виде:

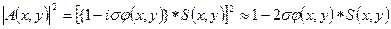. (14)

Рассмотрим влияние аберраций на передаточную функцию оптической системы.

1) Конечные размеры апертуры приводят к тому, что изображение точки имеет вид кружка рассеяния диаметром

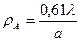(15)

2) Диаметр кружка рассеяния из-за сферической аберрации определяется выражением:

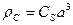, (16)

где C_S- коэффициент сферической аберрации. Величина фазового сдвига при этом

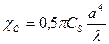. (17)

Коэффициент сферической аберрации всегда больше нуля и чем дальше от оси линзы проходит луч, тем ближе к линзе он пересекает ось линзы.

3) Из-за хроматической аберрации

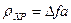, (18)

где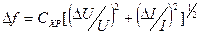

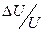(и 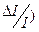- нестабильность ускоряющего напряжения U и тока I.

С_ХР- коэффициент хроматической аберрации.

4) Так как точная фокусировка изображения из-за того. что вид фазового объекта заранее не известен, в реальных случаях приходится учитывать дефокусировку изображения, которая так же и при сферической и хроматической аберрациях приводит к размытию изображения точки в кружок рассеяния:

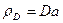, (19)

где D - дефокусировка объективной линзы, расстояние между плоскостью фокусировки и образцом. D>0 при перефокусировке и D<0 при недофокусировке. Соответствующий фазовый сдвиг

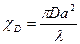. (20)

В современных ПЭМ ВР следует учитывать в первую очередь именно перечисле нные факторы. Тогда предельная разрешающая способность микроскопа, определяемая амплитудной частью аберрации равна:

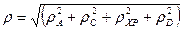. (21) Дополнительный фазовый сдвиг, определяемый в основном 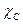и 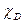равен:

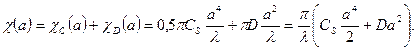
Таким образом, передаточная функция имеет вид:

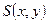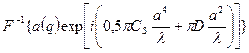=. (22)

Отсюда очевидно, что для малых апертур дополнительный фазовый сдвиг можно минимизировать при отрицательных дефокусировках (D<0). Теперь

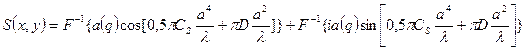(23)

Если контраст амплитудный, то основную роль играет действительная часть ПФ. Однако, при работе с высоким разрешением контраст существенно фазовый, опре-деляемый мнимой частью ПФ. Если направление пучка электронов совпадает с оптической осью микроскопа, сдвиг фазы луча, выходящего из образца под углом к оси, определяется функцией 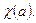Разрешение 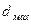~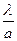. Очевидно, что для получения наилучшего разрешения необходима оптимальная апертура определяемая из условия:

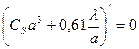
Отсюда оптимальная апертура:

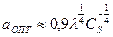. (24)

Соответственно

(25)

Здесь В константа порядка единицы. Оптимальная дефокусировка может быть оценена следующим образом. Определим величину апертуры максимальным вектором дифракции рефлекса участвующего в формировании изображения: 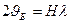. Тогда

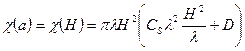(26)

Максимальный контраст в широком диапазоне периодичностей (значений Н) достигается в том случае, когда ПФ имеет плато на зависимости от Н является чисто мнимой (см.23), что достигается при отрицательных значениях дефокусировки (D<0).

Современные ПЭМ ВР при выше описанных условиях минимизации аберраций имеют разрешение, достаточное для наблюдения интерференционной картины, отвечающей кристаллической структуре объектов При этом образец должен быть чисто фазовым.

Несколько примеров интересных областей применения ПЭМ ВР.

1. Анализ дефектов решетки кристаллов, структуры ядра дислокаций, структуры ассоциаций точечных дефектов, структуры границ зерен, двойников и т.д.

2. Выявление особенностей структуры сложных решеток, или прямой анализ сложных крис- таллических структур в сочетании с рентгеноструктурными исследованиями, изучение антифазных доменов политипных структур. Выше было сказано, что условием получения прямого изображения периодической структуры является прохождение через апертурную диафрагму нескольких сопоставимых по интенсивности дифрагированных пучков, которым векторы дифракции Н_J. Если изображение формируется с участием нулевого рефлекса –светлопольное изображение, если без нулевого рефлекса – светлопольное изображение (рис.28). Если пренебречь аберрациями, то амплитуда суммарной волны на сфокусированном изображении имеет вид:

,

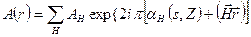где А_Н-амплитуды дифрагированных пучков на выходе из объекта;

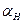-фазовый фактор, отвечающий изменению фазы волны при прохождении объекта s, -характеризует отклонение от условий Брэгга данной системы отражающих плоскостей,

Z-толщина образца;

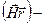изменение фазы луча после за счет отражения после выхода из образца.

Если s=0, фазовый фактор .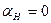

Рассмотрим простейший случай, когда на выходе из кристалла имеются два пучка, например, нулевой и пучок, отраженный от плоскостей, которым отвечает вектор дифракции Н. В этом случае

.

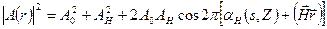Отсюда очевидно, что контраст максимален, если 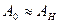, что отвечает толщине Z 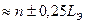, особенно при n=0. Для того, чтобы изображение с полосами максимумов и минимумов с периодом Н^-1 могло быть легко интерпретировано необходимо, чтобы аберрации были скомпенсированы и малы. Это реализуется при малых толщинах. Обычно сопоставляют экспериментальные изображения и рассчитанные по динамической теории. Из экспериментальных условий важным является, чтобы ориентировка была строго симметрична, при этом интенсивности рефлексов,расположенных на электронограмме симмет- рично относительно оси системы должны быть близки.

Наблюдение доменных структур.

Возможность наблюдения ферромагнитных доменов основана на том, что электрон, проходящий через ферромагнитную фольгу, отклоняется магнитным полем доменов благодаря возникновению силы Лоренца, пропорциональной векторноиму произведению 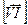, где 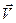-вектор скорости электрона, 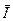-вектор намагниченности домена. Отклонение электронов полями доменов можно использовать для наблюдения последних несколькими способами.

Рассмотрим фольгу со 180-градусными доменами, в которых векор намагниченности параллелен плоскости фольги и междоменной стенке. Поскольку в соседних доменах вектор 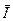имеет противоположные направления, то сила Лорерца отклоняет электроны в противоположные стороны. Это приводит к тому, что рефлексы на электронограмме (в плоскости первичного изображения) расщепляется. А в плоскости изображения пучки, прошедшие соседние домены, будут или перекрываться или расходиться. Очевидно, что на нижней грани фольги пучки перекрываются или расходятся очень слабо. Поэтому, чтобы это увидеть, необходимо рассматривать не изображение нижней грани фольги, которое обычно получается в плоскости изображения; проекционная система должна переносить на экран дефокусированное изображение, расположенное на некотором расстоянии от сфокусированного (плоскость АВ на рисунке 29). Кроме того, можно уменьшить апертурную диафрагму или сместить ее так, чтобы один из двух расщепленных пучков, составляющих рефлекс, формирующий изображение, отсекался диафрагмой. Тогда домены на изображении будут иметь разную освещенность, причем более темными будут те, которые соответствуют пучку, отрезанному диафрагмой. Этот метод позволяет наблюдать сфокусированное изображение доменов. Домены будут видны при условии, что внешнее магнитное поле объективной линзы недостаточно для намагниченности образца до насыщения, когда он станет однодоменным. Поэтому при наблюдении доменов пользуются двумя приемами:

1) микроскоп работает с выключенной объективной линзой и увеличение микроскопа определяется только увеличением его проекционной системы;

2) образец помещают на несколько большем расстоянии от объективной линзы, где магнитное поле достаточно мало; при этом, чтобы сфокусировать изображение, увеличивают фокусное расстояние объектива, что, хотя и уменьшает несколько полезное увеличение микроскопа, позволяетв сопросежн наблюдать такие дефекты как дислокации одновременно с доменными стенками. Одновременное же наблюдение электроннодифракционных картин позволяет связать магнитную структуру образца с его кристаллографической структурой.

Если в кристаллах преход в ферромагнитное, антиферромагнитное или сегнетоэлектричес- кое состояние сопровождается изменением размеров элементарной ячейки, то различным образом ориентированным доменам будут соответствовать разные условия дифракции электронов. В этом случае домены могут наблюдаться и с помощью дифракционного контраста, так как условия дифракции в различных доменах за счет разных величин вектора s будут различными.

Дата добавления: 2014-01-13