Пример 1. Чему равно ускорение Луны и ка­ково отношение этого ускорения к ускорению свободного падения на поверхности Земли?

Чему равно ускорение Луны и ка­ково отношение этого ускорения к ускорению свободного падения на поверхности Земли?

Решение: Используя формулу для центро­стремительного ускорения, находим, что уско­рение Луны 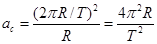, где R -расстоя­ние от Земли до Луны, равное 3,86 • 10⁵ км. Период обращения Луны вокруг Земли T = 27,3 суток или 2,36 -10⁶ с. Подставляя эти зна­чения в выражение для а, имеем а = 2,73-10^-3 м/с².

Вблизи поверхности Земли ускорение равно g = 9,8 м/с².

Таким образом, отно­шение а/g = 1/3590 = (1/60)².

Ньютон выполнил простые вычисле­ния, близкие к описанным в примере 1, и обнаружил, что сила тяготения, дей­ствующая со стороны Земли на яблоко, удаленное к Луне, уменьшится в 3600 = (60)² раз, что соответствует отношению квадратов расстояний.

Отсюда Ньютон за­ключил, что сила тяготения между двумя телами должна убывать обратно пропор­ционально квадрату расстояния между ни­ми.

Он предложил универсальный закон гравитационного притяжения между любыми двумя телами:

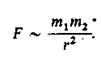
Для обозначения коэффициента пропор­циональности используется прописная буква G. Таким образом,

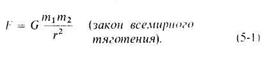
Пример 2.

Предположив, что средняя плотность Земли равна ρ = 5 • 10³ кг/м³, Ньютон нашел численное значение G. (Его догадка с точностью 10% совпала с истинным значением.) Получите выражение для G через ρ, r_з и g.

Решение: Применим формулу (5-1)

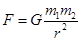
к силе, дей­ствующей между Землей и яблоком.

Обозначим массу Земли М _з,

а массу яблока т.

Тогда

F = G М_з т/ r².

Полагая r равным расстоянию r_з между цент­ром Земли и яблоком, имеем

F= G М_з т / r_з ².

В соответствии со вторым законом Ньютона эта сила должна равняться та, причем в нашем случае а = g. Таким образом,

G М_зт / r_з ² = mg,

откуда

G=gR²_з /M_з.

Учитывая, что M_з равна произведению плотно­сти на объем, т. е.

М _з = ρ (4/3) π R³_з, получаем

G= 3gR²_з / 4ρ π R³_з = 3g / 4ρ π R_з

Подставляя сюда R_з = 6,37-10⁶ м и ρ = 5 х 10³ кг/м³, имеем

G = 7,35- 10^-11 Н -м² •кг ^-2,

что всего лишь на 10% превышает принятое значение

G = 6,67. 10^-11 Н -м² •кг ^-2

Сравнивая ускорение свободного паде­ния на Луне с величиной этого ускорения на поверхности Земли, Ньютон предполо­жил, что Земля ведет себя так, как если бы вся ее масса была сконцентрирована в центре. Ньютон догадался, что такое по­ведение справедливо в случае сил, изме­няющихся обратно пропорционально ква­драту расстояния. Однако ему удалось получить строгое доказательство лишь 20 лет спустя.

«Взвешивание –Земли»

Тяготение действует на огромных рас­стояниях.

Но закон Ньютона утверждает, что взаимно притягива­ются все предметы.

А правда ли, что любые два предмета, притягивают друг друга?

Можем ли мы сами поставить та­кой опыт, а не гадать, глядя на небо, притягиваются ли планеты?

Такой прямой опыт сделал Кавендиш (1731 —1810) при по­мощи прибора, который показан на рис. 11. Идея состояла в том, чтобы подвесить на очень тонкой кварцевой нити стержень с двумя шарами и затем поднести к ним сбоку два больших свинцовых шара, как показано на рисунке. При­тяжение шаров слегка перекрутит нить — слегка, потому что силы притяжения между обычными предметами очень слабы. Силу притяжения между двумя шарами можно из­мерить. Кавендиш назвал свой опыт «взвешиванием Земли».

Педантичный и осторожный преподаватель наших дней не позволит студентам так выразиться; нам пришлось бы ска­зать «измерение массы Земли». При помощи такого прибора Кавендишу удалось непосредственно измерить силу, рас­стояние и величину обеих масс и, таким образом, опреде­лить постоянную тяготения G.

Вы скажете: «Взвешивание Земли представляет собой почти такую же задачу. Мы знаем силу притяжения, знаем массу объекта, который притя­гивается, и знаем, насколько он удален, но мы не знаем ни массы Земли, ни постоянной тяготения, а только их произведение».

Измерив постоянную и зная, как Земля притя­гивает предметы, мы сможем вычислить ее массу.

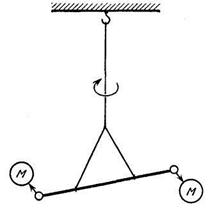
Рис. 11

Этот опыт впервые позволил косвенно определить, на­сколько тяжел, массивен шар, на котором мы живем. Ре­зультат его невольно вызывает удивление, и именно поэтому Кавендиш назвал свой опыт «взвеши­ванием Земли», а не «опре­делением постоянной урав­нения тяготения».

Дата добавления: 2014-01-13