Основы эконометрики

Эконометрика – экономико-математическая наука, которая на основе социально-экономических статистических данных изучает методику построения экономических моделей для отображения закономерностей, количественных связей, динамики социально-экономических процессов с целью прогнозирования, анализа взаимовлияния явлений и принятия оптимальных решений касающихся планирования и т.п.

Каким же образом проводится эконометрический анализ? То есть, какова методология? В широком смысле слова методология эконометрики включает в себя следующие шаги:

1. Утверждение теории или гипотезы.

2. Спецификация (уточнение или выбор) математической модели теории.

3. Спецификация эконометрической модели теории.

4. Сбор данных.

5. Вычисление (получение) параметров эконометрической модели.

6. Проверка гипотез.

7. Прогнозирование или предсказание.

8. Использование модели для управления или политических целей.

Чтобы проиллюстрировать выше указанные шаги, рассмотрим хорошо известную теорию потребления Кейнса.

1. Утверждение теории или гипотезы. Кейнс утверждает, что расходы людей, как правило, и в среднем, увеличиваются с увеличением доходов, но не настолько чтобы превысить их доходы. То есть, граничная склонность к потреблению (marginal propensity to consume, MPC) больше нуля, но меньше единицы.

0< MPC <1.

2. Спецификация математической модели потребления. Можно предположить, что зависимость между расходами и доходами линейна, т.е. может быть представлена следующей формулой

, ,

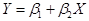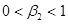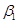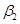в которой Y обозначает расходы, X – доходы, а и – некоторые параметры модели, определяемые на основе данных.

3. Спецификация эконометрической модели потребления. Выше приведенная формула предполагает, что существует точная связь между расходами и доходами. Но очевидно, что эта зависимость будет изменяться от человека к человеку. Чтобы учесть эту неточность в выше приведенном математическом соотношении, его переписывают в таком виде

,

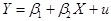где u – так называемый возмущающий член, который является случайной (стохастической) величиной. Эта величина включает все те факторы, которые влияют на потребление, но, ради простоты, не приняты в расчет.

1. Неясность теории: Теория (если она вообще существует), определяющая характер Y, может быть (что чаще всего и случается) неполной. Мы можем знать наверняка, что недельный доход X семьи влияет на ее потребительские расходы Y, однако мы можем не знать или не быть уверенными во влиянии на Y других переменных. Следовательно, u_i может быть использована как замена для всех исключенных или опущенных в модели переменных.

2. Недоступность данных: Даже если нам и известно, что собой представляют некоторые из исключенных из модели переменных и, следовательно, рассматриваем множественную, а не простейшую регрессию, нам может быть недоступна количественная информация по этим переменным. В эмпирических исследованиях очень часто случается так, что данные, необходимые нам в идеале, оказываются недоступными. Например, в принципе мы могли бы ввести в модель в дополнение к доходу в качестве поясняющей переменной накопленные сбережения семьи. Но, к сожалению, информация о денежных сбережениях семьи оказывается недоступной. Следовательно, мы вынуждены исключить эту переменную из модели вопреки тому, что она в значительной степени оказывает влияние на объяснение потребительских расходов семьи.

3. Главенствующие переменные против периферийных переменных: Предположим, что в нашей модели потребительские товары - доход кроме дохода X ₁, учитывается количество детей в семье X ₂, пол X ₃, вероисповедание X ₄, уровень образования X ₅, географический регион проживания X ₆, которые также влияют на уровень потребительских расходов. Но вполне возможно, что суммарное влияние всех или некоторых из этих переменных может быть столь незначительным, что с точки зрения их вклада и ввиду усложнения их не стоит включать в модель в явном виде. Можно надеяться, что их суммарное влияние учитывается как случайная величина u_i.

4. Присущая природе человека случайность: Даже если нам удалось ввести в модель все относящиеся к делу переменные, все равно остается присущая индивидуальному значению Y случайность, которую, как бы мы ни старались, объяснить невозможно. Возмущающий член u может очень хорошо отражать эту присущую случайность.

5. Слабое доверие к переменным: Хотя классическая регрессионная модель предполагает точное измерение переменных Y и X, на практике данные могут быть подвержены ошибкам измерения. Рассмотрим, например, хорошо известную модель Мильтона Фридмана функции потребления. Он считает постоянное потребление (Y ^p) функцией постоянного дохода (X ^p). Но поскольку данные по этим переменным не являются доступными непосредственно, на практике мы используем заменяющие их переменные, такие, как текущее потребление (Y) и текущий доход (X), по которым данные доступны непосредственно. Поскольку доступные данные по Y и X не обязательно должны совпадать с данными по переменным Y ^p и X ^p, то существует проблема погрешности измерения. Возмущающий член u может при этом представлять ошибку измерения. Как мы увидим далее, наличие погрешности измерения серьезно сказывается на точности определения коэффициентов b.

6. Принцип наибольшей простоты: Следуя известному тезису о том, что модель нужно сохранять в наиболее простом виде, пока не доказана ее неадекватность, является естественным желание сохранить регрессионную модель в наиболее простом виде. Если мы можем объяснить характер Y достаточно обстоятельно с помощью двух или трех поясняющих переменных и если наша теория не предполагает твердо, другие переменные должны быть включены в модель, зачем их тогда вводить? пусть u_i заменяет собой все остальные переменные. Конечно, не следует и исключать из модели относящиеся к делу переменные лишь ради сохранения ее простоты.

7. Неверный вид функциональной зависимости: Даже если мы имеем теоретически корректно описывающие явление поясняющие переменные, а также имеем верные относящиеся к этим переменным данные, очень часто мы не знаем вида функциональной зависимости между регрессантом и регрессорами. Является ли функция потребительских расходов линейной по отношению к доходу или нелинейной? В двухмерном регрессионном анализе представление о виде функциональной зависимости может быть получено из графика. Во множественном регрессионном анализе оказывается нелегко определить правильный вид функциональной зависимости, поскольку невозможно визуально составить представление о ней.

4. Сбор данных. Сбор надежных данных является задачей экономической статистики.

5. Вычисление параметров эконометрической модели. Подробный алгоритм вычисления параметров 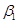и 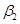будет изложен ниже. Отметим только, что метод вычисления этих параметров называется регрессионным анализом. На основе выше приведенных данных можно получить следующие значения: 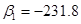и .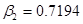

6. Проверка гипотез. Полагая, что полученная модель удовлетворительно описывает действительность, необходимо разработать критерии, которые позволят выяснить насколько хорошо согласуются теоретические данные с экспериментальными.

7. Прогнозирование или предсказание. Если полученная модель подтверждает гипотезы, то ее можно использовать для предсказания будущих расходов на основе ожидаемых величин доходов.

8. Использование модели для управления или политических целей. Предположим, что расходы в 4000 будут поддерживать уровень безработицы в 6.5%. Какой уровень доходов обеспечит такой уровень расходов? Эта величина может быть найдена из уравнения

,

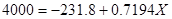откуда 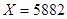. Т. е., при таком уровне доходов расходы составят 4000. Очевидно, что эти данные могут быть использованы в политических целях. Например, соответствующей налоговой политикой правительство может контролировать уровень доходов и, тем самым, получить желаемый уровень расходов.

Основным инструментом эконометрики является регрессионный анализ.

Историческое происхождение термина «регрессия». Впервые термин «регрессия» был введён Френсисом Галтоном, который установил следующее: хотя и существует тенденция к тому, что у высоких родителей рождаются высокие дети, а у невысоких - невысокие, средний рост детей, рожденных от родителей определённого роста, имеет тенденцию смещаться (“регрессировать”) в сторону среднего роста в популяции в целом. Другими словами рост детей необычно высоких родителей и необычно низких имеет тенденцию смещаться в сторону среднего роста популяции. Друг Галтона Карл Пирсон по результатам собранных им данных о росте в группах семей подтвердил закон об универсальной регрессии. Он установил, что средний рост сыновей из группы высоких отцов был меньше, чем средний рост их отцов, а средний рост сыновей из группы низких отцов был больше среднего роста группы отцов, то есть высокие и низкие сыновья “регрессировали” в сторону среднего роста мужчин. Галтон охарактеризовал это явление, как регрессию в сторону обыденности.

Современный смысл, вкладываемый в термин регрессия, несколько иной. В достаточно широком смысле слова можно сказать, что регрессионный анализ связан с изучением зависимости одной (зависимой, поясняемой) переменной от одной или более других (поясняющих) переменных, с целью вычисления и/или прогнозирования средней величины первой при известных (фиксированных) значениях последних.

1. Ключевым понятием, лежащим в основании регрессионного анализа является концепция популяционной регрессионной функции PRF, которая характеризует зависимость на уровне популяции или, говоря языком статистики, в генеральной совокупности. Однако в реальной практической ситуации мы не имеем в своем распоряжении полной совокупности данных для исследования.

ГИПОТЕТИЧЕСКИЙ ПРИМЕР

Как указывалось ранее, регрессионный анализ занимается главным образом вычислением и/или прогнозом средней величины зависимой переменной при фиксированных или предполагаемых значениях поясняющих переменных. Чтобы понять, как это делается, рассмотрим гипотетический пример. Представим себе гипотетическую страну с общим населением в 60 семей. Предположим, что нас интересует изучение связи между недельными потребительскими расходами Y и недельным доходом X после выплаты налогов. Более конкретно, предположим, что мы хотим спрогнозировать средние недельные потребительские расходы, зная недельный доход семьи. Предположим, что мы разделили эти 60 семей на 10 групп с приблизительно равным доходом и исследуем потребительские расходы в каждой группе. Гипотетические данные приведены в таблице 1.

В качестве иллюстрации положим, что нам была известна не вся информация из таблицы 1, а лишь ее часть, полученная путём случайной выборки. Полученная таким образом информация представлена в таблице 2 (слайды).

Вопрос заключается в следующем: можем ли мы по выборочным данным таблицы 2 оценить средние недельные потребительские затраты по всей популяции? Иными словами, можем ли вычислить PRF по выборочным данным?

2. Мы будем рассматривать далее случай линейной PRF, т.е. функции, являющейся линейной относительно неизвестных параметров.

3. Для эмпирических построений важным является то, что PRF является стохастической функцией. Стохастический возмущающий член u_i играет ключевую роль при оценке PRF.

4. PRF представляет собой идеализированный объект, поскольку не представляется возможным получить необходимые сведения по всей популяции. В общем случае исследователь имеет данные наблюдений по некоторой выборке из популяции. Следовательно, исследователь использует выборочную регрессионную функцию SRF для оценки PRF.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.

Основным методом для получения параметров линейной регрессии (регрессионного анализа) является метод наименьших квадратов (МНК), который был предложен Карлом Фридрихом Гауссом – немецким математиком. Чтобы понять этот метод, мы вначале объясним принцип наименьших квадратов.

Вспомним двухмерную PRF:

.

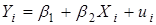Как нами было отмечено ранее, PRF не является объектом, который можно получить прямо. Мы оцениваем его из выборочной регрессионной функции (SRF):

,

,

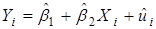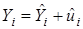где 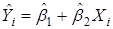представляет оцененную величину .

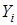Но как определить саму SRF? Чтобы разобраться с этим поступим следующим образом. Перепишем уравнение в виде:

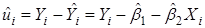, который подсказывает, что 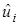(остатки) представляют собой разницу между действительной и оцененной величиной Y.

Теперь для данных N пар наблюдений над Y и X, мы хотели бы определить SRF таким образом, чтобы она была расположена как можно ближе к действительным Y. Для этого можно принять следующий критерий: Выберем SRF таким образом, чтобы сумма остатков 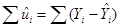была насколько возможно мала.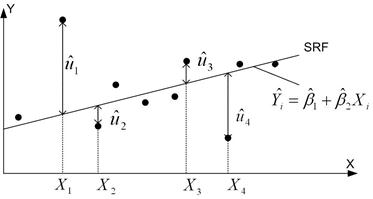

Рис. 1. Критерий наименьших квадратов

При критерии минимума 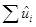возможна ситуация, когда сумма остатков мала, но 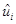широко разбросаны вокруг линии SRF. Однако это невозможно при выборе критерия минимума суммы квадратов остатков, поскольку, чем больше 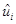(по абсолютной величине), тем больше .

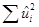Из курса высшей математики известно, что функция 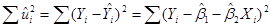будет принимать наименьшее значение при тех числовых значениях 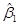и 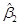, при которых обращаются в ноль частные производные

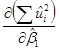и .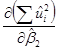

, .

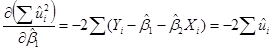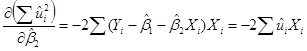Приравнивая нулю эти выражения, получаем следующую систему двух линейных алгебраических уравнений относительно коэффициентов регресси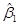и и :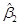

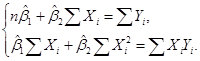
Решив систему уравнений методом Крамера, получим значения параметров регрессии:

, .

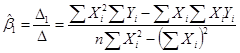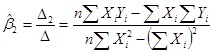Можно получить более простые выражения для коэффициентов регрессии, для этого введем новые величины – отклонения от средних по выборке значений:

, ,

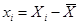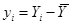После ряда упрощений и преобразований получим формулы коэффициентов:

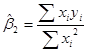
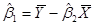
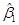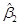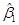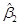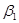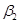Если бы нашей целью было бы только получение оценок и , то всё изложенное исчерпывало бы вопрос. Но мы помним, что в регрессионном анализе нашей целью является не только получение и , а и заключение об истинных величинах и . Например, нам хотелось бы знать насколько близк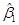и и 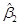к их аналогам по всей популяции или насколько близко 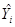к истинному .

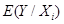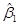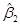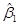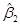Оценщики и по МНК представляют собой функцию от данных выборки. Но поскольку данные могут изменяться от выборки к выборке, то будут меняться и значения оценщиков. Следовательно, необходима мера «достоверности» или точности вычисления оценщиков и . В статистике точность оценщика измеряется его стандартной погрешностью. Оценщики по МНК имеют следующие значения дисперсий и стандартной погрешности

, ,

, .

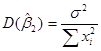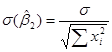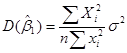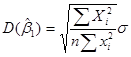Здесь 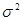представляет собой дисперсию 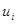. Все величины, за исключением 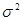можно подсчитать по данным выборки. Для самой же величины 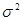справедлива формула:

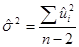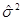, где представляет собой оценку по МНК истинного значения 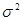. Величина (N–2) носит название числа степеней свободы (df). 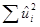представляет собой сумму квадратов остатков RSS (residual sum of squares).

Поскольку 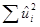известна, то 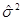может быть легко подсчитана. Сама величина 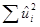может быть подсчитана по формуле 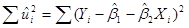или по следующей формуле:

.

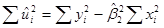Положительный квадратный корень из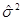

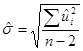
носит название стандартной погрешности оценщика. Она представляет собой стандартное отклонение величин Y от оцененной линии регрессии и часто используется в качестве суммарной меры «качества подгонки» оцененной линии регрессии.

КОЭФФИЦИЕНТ ДЕТЕРМИНИРОВАННОСТИ 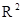: МЕРА «КАЧЕСТВА ПОДГОНКИ».

Обратимся сейчас к рассмотрению вопроса качества подгонки линии регрессии ко множеству данных, т.е. мы исследуем, насколько «хорошо» линия выборочной регрессии подходит к этим данным. Если бы все наблюдения находились на линии регрессии, мы получили бы «точную» подгонку, но на практике это крайне редкий случай. В общем случае будут как положительные отклонения 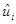, так и отрицательные. Мы стремимся, чтобы эти остатки были насколько возможно малы. Коэффициент детерминированности 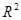представляет суммарную меру качества подгонки линии регрессии к данным наблюдения.

Для подсчета коэффициента 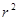поступим следующим образом. Вспомним, что

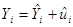
или в форме отклонений

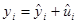. (1)

Возводя обе части этого равенства в квадрат и суммируя, получим

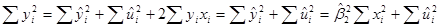, (2)

поскольку 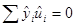и .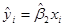

Входящие в (2) различные суммы квадратов могут быть описаны следующим образом: 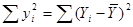– общая дисперсия величины Y относительно средней величины по выборке, называемой общей суммой квадратов TSS (total sum of squares); 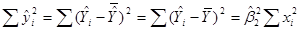– дисперсия оцененной величины Y относительно ее среднего значения (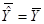) или поясненная сумма квадратов по уравнению регрессии ESS (explained sum of squares). 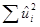– остаточная или не пояснённая дисперсия величины Y относительно линии регрессии или просто остаточная сумма квадратов RSS (residual sum of squares). Таким образом, из (2) получаем равенство

TSS=ESS+RSS (3)

Это равенство показывает, что общая вариация наблюдаемых величин Y относительно их среднего может быть разбита на две части, одна соответствует линии регрессии, а вторая случайным отклонением, поскольку не все наблюдаемые Y лежат на линии регрессии. На рис. 2 это разбиение пояснено геометрически.

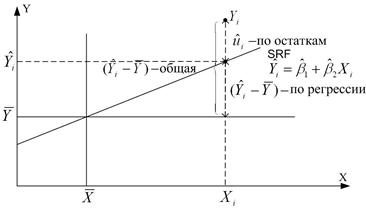
Рис. 2. Разбиение вариации 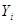на две компоненты.

Разделив обе части (3) на TSS, получаем

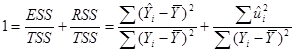. (4)

Определим теперь коэффициент детерминированности 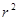следующим образом:

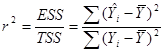(5)

или в альтернативном виде

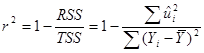. (5а)

Определенная таким образом величина 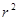известна как коэффициент детерминированности и является наиболее широко используемой мерой качества подгонки линии регрессии.

Отметим следующие два свойства :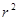

Коэффициент 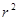неотрицателен (Следует из выражения (5)).

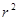ограничен пределами 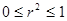. При значении 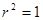мы имеем случай точной подгонки, т.е. 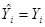для каждого i. С другой стороны, случай 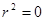означает отсутствие связи между регрессантом и регрессором.

Хотя 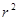можно подсчитать непосредственно по формулам (5), (5а), проще воспользоваться следующими формулами:

.

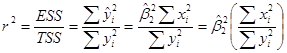Разделив числитель и знаменатель на размер выборки N (или N–1, если размер выборки мал), получаем:

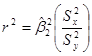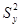, где и 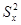представляют выборочные дисперсии по Y и Х, соответственно.

Поскольку 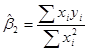, уравнение можно представить в виде:

.

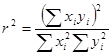Используя выражения для 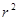, мы можем выразить ESS и RSS следующим образом:

,

.

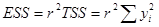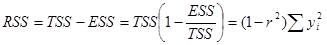Следовательно, мы можем записать: TSS=ESS+RSS,

.

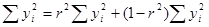Количественно близко связанная с 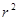, но концептуально отличающейся является величина коэффициента корреляции, представляющего степень ассоциативности между двумя переменными. Его можно подсчитать по любой из формул:

.

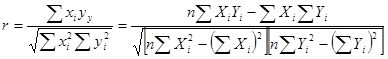Определенная таким образом величина носит название коэффициента корреляции по выборке.

Вот некоторые его свойства:

Он может быть положительным или отрицательным, знак r зависит от знака числителя, являющегося мерой ковариации по двум выборкам переменных.

Он лежит между –1 и 1, т.е. .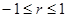

По своей природе он симметричен, т.е. коэффициент корреляции между Х и Y (rXY) тот же, что и между Y и Х (rYX).

Коэффициент корреляции является мерй только линейной ассоциативности или линейной зависимости; он неприменим для описания нелинейной зависимости. Так, на рис. 3, Y=X2 – точная зависимость, хотя .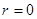

Хотя r является мерой линейной ассоциативности между двумя переменными, это необязательно подразумевает какую-либо причинно-следственную связь, как было отмечено ранее.

(а) (б) (в)

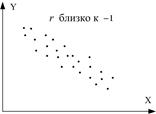
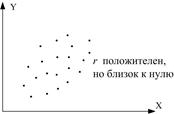
(г) (д) (е)

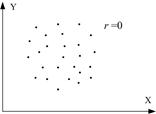
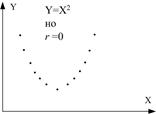
(ж) (з)

Рис. 3. Корреляционный коэффициент для разных случаев выборок.

В контексте регрессии 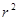более информативен, чем r, поскольку 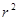говорит нам о доле вариации в зависимой переменной, объясняемой поясняющей переменной.

В заключении заметим, что коэффициент детерминированности 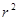может быть подсчитан как квадрат коэффициента корреляции между переменным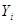и и 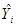по следующей формуле

.

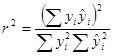ИНТЕРВАЛЬНЫЕ ОЦЕНКИ: ОСНОВНЫЕ ИДЕИ.

Для демонстрации подхода рассмотрим гипотетический пример «семейный доход-расход на потребительские товары», приведенный ранее. Уравнение 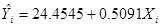показывает, что предельная склонность к потреблению 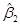равна 0.5091. Насколько эта оценка достоверна? Вследствие случайности выборки точечное значение, скорее всего, отличается от истинного . В статистике достоверность точечного значения измеряется его стандартной ошибкой. Следовательно, вместо того, чтобы полагаться лишь на точечное значение, мы можем построить интервал вокруг точки оценивания, скажем в две или три стандартные ошибки влево и вправо от точки, так что этот интервал содержит, скажем, с вероятностью 95%, истинное значение параметра. В этом заключается, грубо говоря, идея интервальной оценки.

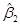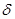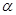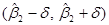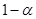Более точно, предположим, что мы хотим найти насколько «близко» расположена к. Для этого попробуем найти такие два положительные числа и, лежащие между 0 и 1, что случайный интервал содержит истинное значение с вероятностью . В математических обозначениях это записывается следующим образом

.

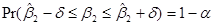Такой интервал, если он, конечно, существует, носит название доверительного интервала: 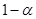называется доверительным коэффициентом, а 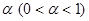известен как уровень (степень) значимости. Концы доверительного интервала называются границами доверия, 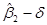– нижняя граница доверия и 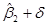– верхняя граница доверия. На практике 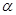и 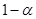часто выражается в процентах.

Уравнение показывает, что в противоположность очечной оценке, интервальная оценка представляет собой интервал, построенный таким образом, что он содержит внутри себя с определенной вероятностью (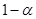) истинное значение параметра. Например, если или 5%, говорит следующее: вероятность того, что случайный интервал содержит истинное значение , равна 0.95 или 95%. Интервальная оценка дает, таким образом, интервал, в котором может лежать истинное значение .

ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ РЕГРЕССИОННЫХ КОЭФФИЦИЕНТОВ 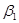И .

Как было отмечено ранее, при допущении о нормальном законе распределения остатков 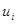полученные по МНК оценк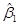и и 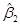сами распределены по нормальному закону с известными математическими ожиданиями и дисперсиями:

, ,

, .

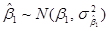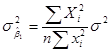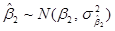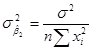Следовательно, например, переменная:

(6)

представляет собой стандартизованную нормальную переменную. Если 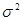известна, то важным свойством нормально распределенной величины с ожиданием 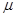и дисперсией 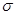есть то, что площадь под плотностью распределения между 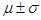составляет 68%, между 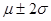– около 95%, а между 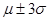– около 99.7%.

На практике 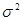известна редко и она заменяется ее несмещенной оценкой 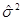. Если заменить в (6) 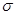на 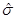, то можно получить

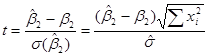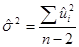, , (7)

где 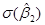представляет собой стандартную ошибку оценщика 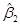. Можно показать, что определенная таким образом переменная t подчиняется распределению Стьюдента с N–2 степенями свободы. Следует обратить внимание на разницу между (6) и (7). Следовательно, вместо того, чтобы использовать нормальное распределение, мы можем использовать распределение Стьюдента для построения доверительного интервала величины :

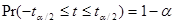, (8)

где t определяется формулой (7), а 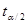представляет собой величину распределения Стьюдента для 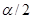уровня значимости и N–2 степени свободы. Она часто называется критической величиной при 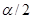уровне значения. Подстановка (7) в (8) дает равенство:

.

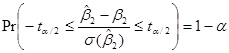Преобразуя, получаем:

.

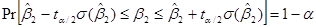Это равенство представляет 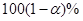доверительный интервал для , который может быть записан более компактно в виде

.

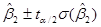По аналогии с этим мы можем записать доверительный интервал для :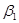

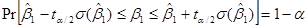
ПРОВЕРКА ГИПОТЕЗ: ОБЩИЕ ЗАМЕЧАНИЯ.

Проблема проверки статистических гипотез может быть сформулирована следующим образом: согласуется ли данное наблюдение или заключение с некоторой сформулированной гипотезой или нет? Используемый термин «согласовываться» следует понимать в смысле «достаточной» близости к величине, о которой идет речь в гипотезе так, что мы не отвергаем эту гипотезу. Так, если некоторая теория или опыт приводит нас к убеждению, что истинное значение углового коэффициента в примере «потребление-доход», равно единице, является ли полученное 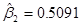из расчетов по данным из выборки в таблице 2 соответствующим гипотезе? Если это так, мы не отвергаем гипотезу; иначе мы можем ее отвергнуть.

На языке статистики высказанная гипотеза носит название нулевой гипотезы и обозначается символом Н0. Нулевая гипотеза проверяется альтернативной гипотезой обозначаемой Н1, которая может утверждать, например, что истинное не равно единице. Альтернативная гипотеза может быть простой или составной. Например, Н1: 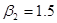– простая гипотеза, а Н1: 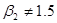– составная.

Теория проверки гипотез занимается развитием методов или процедур для решения вопроса отвергнуть или нет нулевую гипотезу. Существует два взаимно дополняющих друг друга подхода для разработки таких правил, называемые доверительный интервал и проверка значимости. Оба этих подхода считают, что рассматриваемая переменная (статистика или оценщик) имеет некоторое вероятностное распределение и проверка гипотез включает высказывание заявления о величинах параметров таких распределений. Например, мы знаем, что при допущении о нормальном распределении 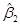имеет математическое ожидание . Если мы выдвигаем гипотезу, что 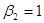, мы делаем допущение об одном из параметров нормального распределения, а именно, о его математическом ожидании. Большинство из рассматриваемых нами далее статистических гипотез будут подобного рода.

ПРОВЕРКА ГИПОТЕЗ: ПОДХОД НА ОСНОВЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА.

Для демонстрации подхода на основе доверительного интервала еще раз обратимся к рассмотренному примеру «потребление-доход». Как мы знаем, оценка МРС 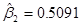. Предположим, мы полагаем, что:

, ,

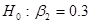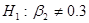т.е. по нулевой гипотезе истинное значение равно 0.3, а по альтернативной – меньше или больше этого значения. Соответствует ли полученное 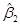гипотезе Н0? Чтобы ответить на этот вопрос, обратимся к доверительному интервалу:

.

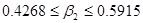Мы знаем, что в длинной череде подобных интервалов будет содержаться с вероятностью 95%. Следовательно, последовательность интервалов определяет пределы, в которых истинное может попадать с доверительным коэффициентом, скажем, 95%. Таким образом, доверительный интервал представляет множество соответствующих нулевой гипотезе интервалов. Следовательно, если из гипотезы Н0 попадает внутрь интервала с 100(1–α)% вероятностью, то мы не отвергает нулевую гипотезу; если же он лежит вне интервала, мы можем ее отвергнуть.

Правило принятия решения: Постройте 100(1–α)% доверительный интервал для . Если из нулевой гипотезы Н0 попадает внутрь интервала, не отвергайте Н0, если лежит вне интервала, отвергайте Н0.

Следуя этому правилу, для нашего гипотетического примера, при 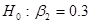мы видим, что с 95% вероятностью лежит вне доверительного интервала. Следовательно, мы можем отвергнуть гипотезу о том, что с 95% доверием истинное значение МРС равно 0.3. В статистике, когда мы отвергаем нулевую гипотезу, говорят, что наше заключение статистически значимо.

ПРОВЕРКА ГИПОТЕЗ: ПОДХОД, ОСНОВАННЫЙ НА ПРОВЕРКЕ ЗНАЧИМОСТИ (t– тест).

Альтернативный по отношению к методу доверительного интервала, но дополняющий его метод проверки статистических гипотез, есть подход проверки на значимость, развиваемый независимо Р.А.Фишером и совместно Нейманом и Пирсоном. В достаточно общем смысле, проверка на значимость есть процедура, с помощью которой результаты выборки используются для проверки истинности или ложности нулевой гипотезы. В качестве иллюстрации, вспомним, что при допущении о нормальности распределение переменной:

,

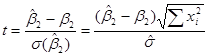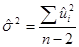
следует распределению Стьюдента с (N–2) степенями свободы. Если истинное значение определено нулевой гипотезой, переменная t может быть без труда подсчитана по имеющимся данным выборки, и, следовательно, она может служить проверке статистики. А поскольку этот тест статистики следует t– распределению, можно записать следующий доверительный интервал:

,

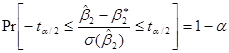где есть величина по определению Н0, а 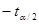и 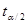критические величины, полученные из таблицы распределения Стьюдента для α/2 уровня значимости и N–2 степеней свободы.

В процедуре построения доверительного интервала мы пытаемся установить область или интервал, в который с определенной вероятностью попадает истинное значение , в то время как в тесте на проверку значимости мы придаем величине некоторое значение и пытаемся определить, лежит ли подсчитанное значение 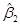в разумной близости от принятой величины для .

На практике можно подсчитать величину 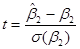, стоящую посередине неравенства и посмотреть лежит ли она между критическими значениями t или нет. Для нашего случая t=5.86, видно, что она лежит в критической области, изображенной на рис. 4.

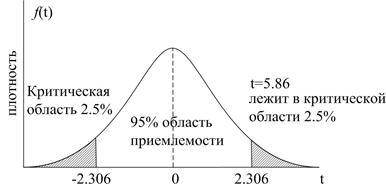
Рис. 4. 95% доверительный интервал для t (8df).

Заметим, что если 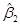равно значению, принятому по гипотезе, то величина t будет равна 0. По мере того, как 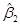будет удаляться от значения, принятого по гипотезе, |t| будет возрастать. Следовательно, «большая» величина |t| служит свидетельством против гипотезы. Конечно, мы всегда можем использовать таблицу распределения Стьюдента для определения того является конкретная величина t большой или малой; ответ, как мы знаем, зависит от числа степеней свободы и от вероятности допустимой ошибки. Поскольку мы используем t– распределение, предыдущая процедура проверки носит соответствующее название t– теста. На языке проверки значимости, о статистике говорят, что она статистически значима, если величина статистики лежит в критической области. В этом случае нулевая гипотеза отвергается. При тех же условиях, о тесте говорят как о статистически не значимом, если величина теста статистики лежит в области приемлемости. В этом случае нулевая гипотеза не отвергается. В нашем примере t– тест является значимым и, следовательно, мы отвергаем нулевую гипотезу.

РЕГРЕССИОННЫЙ АНАЛИЗ И АНАЛИЗ ДИСПЕРСИИ.

Обратимся к регрессионному анализу с точки зрения анализа дисперсии.

Ранее было доказано, что TSS=ESS+RSS, которое разлагает общую сумму квадратов (TSS) на два слагаемых: поясненная сумма квадратов (ESS) и сумма квадратов остатков (RSS). Изучение этих слагаемых в TSS известно под термином (ANOVA, analysis of variance) анализа дисперсии с точки зрения регрессии.

С каждой суммой квадратов связано число ее степеней свободы df, число независимых наблюдений, на которых она основана. TSS имеет (N–1) степень свободы, поскольку мы теряем одну степень при подсчете средней величины выборки 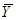. RSS имеет (N–2) степени свободы (т.к. 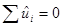, 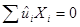). ESS имеет всего одну степень свободы, что следует из факта, что 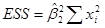есть функция только от 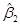, поскольку 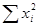известна. Отметим, что указанное число степеней свободы справедливо только для случая уравнения регрессии с двумя переменными.

Поместим перечисленные суммы квадратов и соответствующие им степени свободы в таблицу 3, являющуюся стандартным видом таблицы ANOVA.

Таблица 3.

ANOVA таблица для регрессионной модели с двумя переменными.

Источники дисперсии	SS	df	MSS
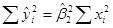
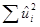
Вследствие дисперсии (ESS)   Вследствие остатков (RSS)		N–2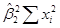
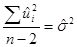
TSS		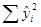N–1

SS обозначает сумму квадратов (sum of squares)

MSS – средняя сумма квадратов (mean sum of squares)

Рассмотрим следующую переменную:

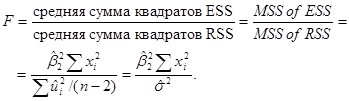
Коэффициент F представляет тест нулевой гипотезы Н0: b2=0. Поскольку все входящие в выражение величины получаются из выборки, коэффициент позволяет проверить гипотезу о том, что b2=0. Все, что необходимо для этого сделать, это подсчитать F и сравнить его с критической величиной F, полученной из таблиц распределения плотности F с выбранным уровнем значимости, или получить р-величину для подсчитанной статистики F.

Для иллюстрации обратимся к нашему примеру «расход-доход». Таблица ANOVA для этого примера представлена ниже.

Источник дисперсии	SS	df	MSS
Вследствие регрессии (ESS)	8552.73		8552.73	F=85552.73/42.159= =202.87
Вследствие остатков (RSS)	337.27		42.159
TSS	8890.00

Из таблицы видно, что подсчитанная величина F=202.87. Величина р, соответствующая этой статистике, с 1 и 8 степенями свободы не может быть получена из таблицы распределения F, но используя электронные компьютерные таблицы можно показать, что эта величина есть 0.0000001, т.е. очень малая величина. Если при проверке гипотез подхода по уровню значимости коэффициент α=0.01 или 1%, то увидите, что подсчитанный коэффициент F=202.87 оказывается значимым для этого уровня. Следовательно, если мы отвергнем нулевую гипотезу о том, что b2=0, то вероятность совершения ошибки I-го типа (отвергается верная гипотеза) очень мала. Следовательно, с большой долей вероятности мы можем сделать вывод о том, что доход Х влияет на расходы и потребление Y.

Таким образом, t и F тесты представляют нам два альтернативных но взаимодополняющих пути проверки нулевой гипотезы о том, что b2=0. Если это так, то почему не ограничиться t тестом и не заботиться о проверке F теста? Оказывается, что для модели с двумя переменными это можно допустить в самом деле. Но для модели множественной регрессии F тест обладает некоторыми интересными приложениями, что делает его очень полезным и мощным методом проверки статистических гипотез.

ПРИЛОЖЕНИЕ РЕГРЕССИОННОГО АНАЛИЗА: ПРОБЛЕМА ПРОГНОЗА.

На основе выборочных данных таблицы 2 нами было получено следующее уравнение выборочной регрессии:

,

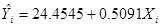где 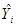– оценщик истинного 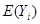, соответствующего данному Х. Какая польза может быть извлечена из этой регрессии? Его (уравнение) можно использовать для «прогноза» или «предсказания» будущих потребительских затрат Y, соответствующих некоторому данному уровню дохода Х. Возможны следующие два вида прогноза:

· прогноз условной средней величины Y, соответствующий выбранному Х, скажем Х0, т.е точки на самой линии популяционной регрессии,

· прогноз индивидуальной величины Y, соответствующей Х0.

Мы будем называть эти два прогноза средним прогнозом и индивидуальным прогнозом.

Дата добавления: 2014-01-13