Индивидуальный прогноз

Если нас интересует индивидуальный прогноз величины Y, Y0, соответствующего заданной величине Х0, то, как показано в приложении 5, раздел 5А.3, лучшая линейная несмещенная оценка Y0 также дается формулой (5.10.1), но ее дисперсия имеет вид

.

Можно показать, что Y0 также подчиняется нормальному закону распределения. Подставляя 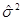вместо неизвестной 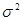можно показать, что

,

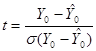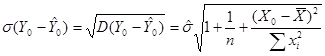
также подчиняется распределению Стьюдента. Следовательно, этот закон распределения может быть использован для вывода заключения об истинном значении Y0. Продолжая исследование модели «потребление-доход», мы видим, что прогнозируемая точка Y0=75.3645 та же что и 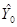, и ее дисперсия:

,

.

Следовательно, 95% доверительный интервал для Y0, соответствующего Х0=100 определяется следующим образом

.

Мы видим, что доверительный интервал для индивидуального Y0 шире, чем при тех же условиях доверительный интервал для среднего значения E(Y|X0). Подсчитывая подобные доверительные интервалы для разных значений Х их таблицы 2, мы получим 95% доверительную область для индивидуальных значений Y при этих значениях Х. Эта доверительная область изображена на том же рис.5, что и доверительная область для .

ФОРМА ОТЧЕТА ПО РЕЗУЛЬТАТАМ РЕГРЕССИОННОГО АНАЛИЗА.

Существуют различные формы отчета по результатам регрессионного анализа, но здесь мы пользуемся следующей формой, относящейся к нашему иллюстрированному примеру:

,

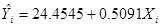s=(6.4138) (0.0357) r2=0.9621

t=(3.8128) (14.2405) df=8 (5/11/1)

p=(0.002571) (0.000000289) F1,8=202.87

В выражениях (5.1.1) числа в скобках во второй строке представляют стандартные ошибки коэффициентов регрессии, числа в скобках в третьей строке представляют оценки величин t

,

в предположении нулевой гипотезы о том, что b1=0 и b2=0 (3.8128=24.4545/6.4138; 14.2405=0.5091/0.0357), а числа в третьей строке есть рассчитанные вероятности. Так, для 8df вероятность получения величины 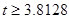равна 0.0026, а вероятность получения 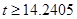получается около 0.0000003.

Путем представления вероятности р оцениваемых коэффициентов, мы можем сразу видеть точный уровень значимости каждой оцениваемой величины t. Так, при нулевой гипотезе Н0: b1=0, точная вероятность (т.е. величина р) получения величины 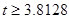примерно равна 0.0026. Следовательно, если мы отвергаем эту нулевую гипотезу, вероятность того, что мы совершаем ошибку I типа состоит в 26 случаях из 10000, в действительности очень малая величина. В задачах, имеющих практическое значение, мы можем сказать, что истинное значение . В еще большей степени это относится к склонности к покупке b2.

Как мы ранее упоминали, 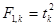. При нулевой гипотезе величина F=202.87 (1df числитель, 8df знаменатель), а t=14.24(8df); в соответствии с теорией (14.24)2=202.87.

Дата добавления: 2014-01-13