Двойственность в линейном программировании

Лекция 6.

Внешняя память

Стек МК

В микроконтроллерах ОЗУ данных используется также для организации вызова подпрограмм и обработки прерываний. При этих операциях содержимое программного счетчика и основных регистров (аккумулятор, регистр состояния и другие) сохраняется и затем восстанавливается при возврате к основной программе.

В фон-неймановской архитектуре единая область памяти используется, в том числе, и для реализации стека. При этом снижается производительность устройства, так как одновременный доступ к различным видам памяти невозможен. В частности, при выполнении команды вызова подпрограммы следующая команда выбирается после того, как в стек будет помещено содержимое программного счетчика.

В гарвардской архитектуре стековые операции производятся в специально выделенной для этой цели памяти. Это означает, что при выполнении программы вызова подпрограмм процессор с гарвардской архитектурой производит несколько действий одновременно.

Необходимо помнить, что МК обеих архитектур имеют ограниченную емкость памяти для хранения данных. Если в процессоре имеется отдельный стек и объем записанных в него данных превышает его емкость, то происходит циклическое изменение содержимого указателя стека, и он начинает ссылаться на ранее заполненную ячейку стека. Это означает, что после слишком большого количества вызовов подпрограмм в стеке окажется неправильный адрес возврата. Если МК использует общую область памяти для размещения данных и стека, то существует опасность, что при переполнении стека произойдет запись в область данных либо будет сделана попытка записи загружаемых в стек данных в область ПЗУ.

Несмотря на существующую тенденцию по переходу к закрытой архитектуре МК, в некоторых случаях возникает необходимость подключения дополнительной внешней памяти (как памяти программ, так и данных).

Если МК содержит специальные аппаратные средства для подключения внешней памяти, то эта операция производится штатным способом (как для МП).

Другой, более универсальный, способ заключается в том, чтобы использовать порты ввода/вывода для подключения внешней памяти и реализовать обращение к памяти программными средствами. Такой способ позволяет задействовать простые устройства ввода/вывода без реализации сложных шинных интерфейсов, однако приводит к снижению быстродействия системы при обращении к внешней памяти.

Вопросы:

1. Понятия двойственности, теневой цены, двойственной оценки.
2. Правила построения двойственной задачи.
3. Основные теоремы двойственности и их экономическое содержание.

1. Понятия двойственности, теневой цены, двойственной задачи.

Двойственность является одним из фундаментальных понятий в линейном программировании, приводящим к важному результату теоретического и практического характера. Рассмотрим понятие двойственности на примере задачи оптимального использования ресурсов.

На производство n видов продукции предприятие затрачивает m видов ресурсов, имеющихся в ограниченных количествах b = (b₁, b₂, …, b_m). На производство единицы j-го вида продукции требуется a_ij единиц i-го вида ресурса. Прибыль от реализации единицы продукции С_j, j = 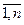. Необходимо определить такой план производства х = (х₁, х₂,…, х_n), при котором прибыль предприятия была бы максимальной. Математическая модель задачи выглядит следующим образом.

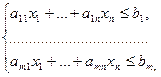С₁х₁ + … + С_nx_n =F(x) m ax, x_j0, j = .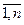

В общем случае задача решается симплекс-методом. Что ограничивает производство? Зададимся вопросом, какова с точки зрения предприятия ценность имеющихся в его распоряжении ресурсов? При решении этого вопроса будем иметь в виду, что ресурсы, которые предприятие не может полностью использовать, имеют для него очень низкую ценность, в том смысле, что предприятие не согласно нести даже небольшие расходы на увеличение запасов этих ресурсов. Дорогое оборудование, не участвующее в технологическом процессе, составляет для предприятия нулевую ценность.

Наибольшую ценность, очевидно, будут иметь те ресурсы, которые в наибольшей степени ограничивают выпуск продукции, а, следовательно, и прибыль предприятия и на увеличение запасов которых предприятие согласно затратить значительные средства.

Можно считать, что каждый вид ресурса обладает некоторой «теневой» ценой, определяющей ценность данного ресурса для предприятия с точки зрения прибыли от реализации выпускаемой продукции и зависящей от наличного количества этого ресурса и потребности в нем.

Кроме того, если сейчас используется один технологический процесс, требующий больших затрат некоторого ресурса, запасы которого ограничены, значит «теневая» цена велика, то завтра этот процесс может быть изменен таким образом, что позволит более экономно использовать все запасы ресурсов, следовательно изменятся «теневые» цены. Но как бы ни усовершенствовался технологический процесс совсем без ресурсов не обойтись. Таким образом, можно предположить, что существуют оптимальные теневые цены, соответствующие оптимальному распределению ресурсов.

В экономической литературе «теневые» цены часто называют объективно-обусловленными или оптимальными оценками, двойственными или учетными, неявными оценками.

Чтобы определить оптимальные «теневые» цены ресурсов необходимо составить и решить задачу оптимизации. Имеем те же исходные данные, что и для задачи оптимального использования ресурсов. Только теперь необходимо найти такие «теневые» цены ресурсов y = (y₁, y₂,…,y_m), при которых стоимость всех ресурсов была бы минимальна, y_i – «теневая» цена единицы i-го ресурса, y_i 0.

«Теневые» цены y = (y₁, y₂,…,y_m) должны быть такими, чтобы «теневая» цена всех ресурсов, затраченных на производство единицы продукции каждого вида, была бы не меньше получаемого от ее реализации дохода. Другими словами, стоимость затраченных ресурсов не может быть меньше стоимости окончательного продукта (так как существуют неизбежные издержки):

.

Дата добавления: 2014-01-13