
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оптимальными «теневыми» ценами естественно считать такие, которые минимизируют общую стоимость ресурсов
|
|
|
|
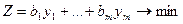 .
.
Запишем обе задачи в матричном виде:
Прямая задача Двойственная задача
Ах  АТy
АТy  C
C
F = CTx  Z =
Z = 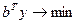
x  0 y
0 y  0
0
Эти задачи называют парой двойственных задач. Пара двойственных задач может быть экономически интерпретирована следующим образом.
Прямая задача: Сколько и какой продукции xj необходимо производить, чтобы при
заданных стоимостях Cj и размерах ресурсов bi максимизировать выпуск
продукции в стоимостном выражении?
Двойственная задача: Какова должна быть цена каждого ресурса yi, чтобы при заданных
количествах bi и стоимостях Cj минимизировать затраты?
- Правила построения двойственной задачи.
Исходя из общего вида прямой и двойственной задач можно установить связь между этими задачами, позволяющую для любой ЗЛП строить двойственную ей задачу.
Свойства двойственных задач (правила).
- Число неизвестных двойственной задачи равно числу ограничений прямой задачи. Число ограничений двойственной задачи равно числу неизвестных прямой задачи.
- Матрица коэффициентов двойственной задачи является транспонированной матрицей коэффициентов прямой задачи.
- Коэффициенты целевой функции двойственной задачи являются свободными членами ограничений прямой задачи.
- Свободные члены ограничений двойственной задачи являются коэффициентами целевой функции прямой задачи.
- Если ограничения прямой задачи записаны со знаком меньше или равно (
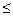 ), то ограничения двойственной задачи записываются со знаком больше или равно (
), то ограничения двойственной задачи записываются со знаком больше или равно ( ).
). - Если ограничение прямой задачи задано в виде уравнения, то соответствующее неизвестное двойственной задачи не ограничено знаком.
- Если какое-либо неизвестное прямой задачи не ограничено знаком, то соответствующее ограничение двойственной задачи будет задано в виде равенства.
- Если целевая функция прямой задачи сформулирована на максимум, то целевая функция двойственной задачи будет сформулирована на минимум.
Существует много различных комбинаций ограничений и целевой функции для записи исходной задачи. Для упрощения задачи построения двойственной задачи запишем прямую задачу в некотором стандартном виде прямой задачи. Этот вид предполагает, что:
1) все ограничения имеют знак 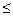 ;
;
2) целевая функция сформулирована на максимум;
3) все неизвестные неотрицательны.
Чтобы записать прямую задачу в стандартном виде, необходимо:
1) неравенство со знаком  умножить на (-1);
умножить на (-1);
2) равенство заменить на два неравенства противоположных знаков, одно из которых следует умножить на (-1);
3) формулировку целевой функции меняют заменой знаков коэффициентов на противоположные;
4) если переменное xj не ограничено знаком, его можно представить в виде разности двух неотрицательных переменных.
Пример. Составить двойственную задачу к исходной.
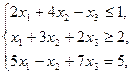
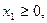

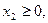
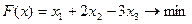 .
.
Решение. 1) Стандартный вид прямой задачи.
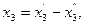
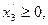
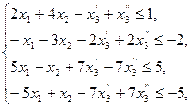
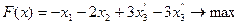
2) Двойственная задача: 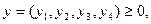
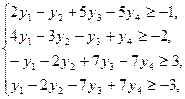
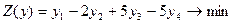
Задачу можно записать в виде, соответствующем исходной прямой задаче,
если заменить: а) 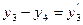 - не ограничена знаком,
- не ограничена знаком,
б) два последних ограничения соответствуют равенству.
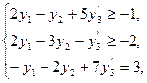
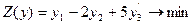 .
.
- Основные теоремы двойственности и их экономическое содержание.
Теорема 1. Двойственная задача к двойственной есть прямая задача.
Доказательство: Пусть имеем пару двойственных задач в матричном виде.
Ах  АТy
АТy  C
C
F = CTx  Z =
Z = 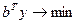
x  0 y
0 y  0
0
Построим к двойственной задаче двойственную:
1) запишем в стандартном виде -АТy  -C
-C
Z = -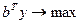
2) -Ах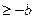 Ах
Ах 
F = - CTx 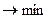 F = CTx
F = CTx 
Что и требовалось доказать.

|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 265; Нарушение авторских прав?; Мы поможем в написании вашей работы!