Дифракция Фраунгофера на круглом отверстии

Случай дифракции на круглом отверстии представляет большой интерес для практики, так как оптические линзы и объективы имеют обычно круглую форму. В случае, когда точечный источник света находится в фокальной точке линзы, выходящий пучок испытывает дифракцию Фраунгофера на апертуре линзы. Это означает, что идеально плоскую световую волну с помощью линзы создать невозможно. По мере удаления от линзы диаметр светового луча неизбежно увеличивается. Это увеличение характеризуют угловой расходимостью светового пучка. Минимальная угловая расходимость светового пучка, выходящего из отверстия, определяется и ограничивается явлением дифракции света.

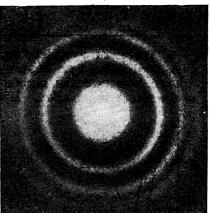
Рис. 11.3. Картина распределения интенсивности на круглом отверстии с резкими кромками при дифракции Фраунгофера.

Для вычисления распределения света на удаленном экране, при дифракции Фраунгофера на круглом отверстии необходимо просуммировать амплитуды лучей, приходящих в заданную точку экрана от всех точек отверстия с учетом фаз световых лучей. При этом для упрощения расчетов естественно перейти к полярным координатам, так как картина дифракции симметрична относительно оптической оси.

Приведем сразу результаты расчета. При малых углах дифракции интеграл выражается через функцию Бесселя первого порядка, которую принято обозначать как J₁(a). В рассматриваемом случае a = kRq = 2pRq/l. R – радиус отверстия, q -угол дифракции.

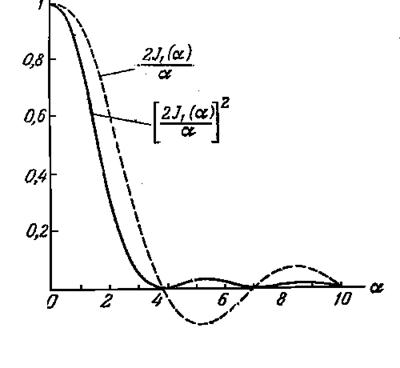
Рис. 11.4. Распределение амплитуды и интенсивности световых колебаний при дифракции Френеля на круглом отверстии с резкими краями.

Нетрудно заметить, что распределение, показанное на рис. 11.4 похоже на картину дифракции Фраунгофера на щели. Приближенно угловой радиус первого минимума интенсивности определяется формулой:

q = 0,61 l/R. (11.3)

Этим углом принято определять дифракционную расходимость излучения для светового пучка радиуса R. Поскольку длина волны всегда значительно меньше размеров апертуры линзы или объектива, то дифракционная расходимость светового пучка диаметром, превышающим миллиметр, чрезвычайно мала и измеряется угловыми секундами.

Обычно считают, что дифракционная расходимость определяемая формулой (11.3), – минимально возможный угол расходимости светового пучка. Однако это не совсем так. Формула (11.3) относится к дифракции на отверстии с резкими кромками. Сглаживание кромок (эту процедуру называют аподизацией отверстия) изменяет распределение интенсивности светового максимума, уменьшает амплитуду дифракционных колец и позволяет вообще говоря уменьшить угловую расходимость пучка по сравнению с дифракционной на отверстии с резкими кромками.

Однако практически аподизация не позволяет существенно уменьшить дифракционную расходимость излучения. Ее применяют главным образом для устранения колец, окружающих главный дифракционный максимум.

Дата добавления: 2014-01-13