Увеличение

Основные формулы идеальной оптической системы

zz` = ff` (18.1)

- формула Ньютона. В случае равенства переднего и заднего фокусного расстояния она принимает вид: zz` = f².

f`/a` + f/a = 1 (18.2)

– формула Гаусса, или формула отрезков. При равенстве переднего и заднего фокусных расстояний она принимает вид:

1/a` + 1/a = 1/f`.

Линейное увеличение b – отношение линейных размеров изображения к линейным размерам предмета –

y`/y = b = - f/z = - z`/f`. (18.3)

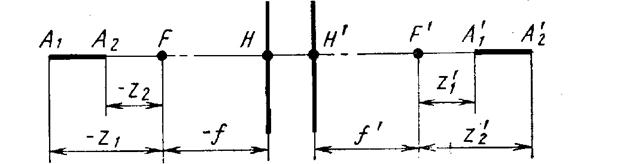
Рис. 18.3. Продольное увеличение оптической системы. Отрезки А₁ А₂ = Dz и А`<sub>1</sub> А<sub>2</sub>`= Dz`, лежащие на оптической оси сопряжен друг с другом. Положение сопряженных точек относительно фокусов определяются отрезками z.

Продольное или осевое увеличение a = - Dz`/Dz.

Пользуясь формулой Ньютона свяжем отрезки с фокусными расстояниям.

z₁` = ff`/z₁; z`<sub>2</sub> = ff`/z₂. Dz` = ff`(1/z₂ – 1/z₁)

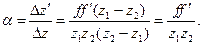
Из равенства (17.7) следует, что z` = - bf`; z = - f/b. Откуда при условии f` = - f находим:

a = b². (18.4)

Продольное увеличение равно квадрату линейного увеличения.

Угловое увеличение идеальной оптической системы – отношение тангенов углов, образованных сопряженными лучами с оптической осью.

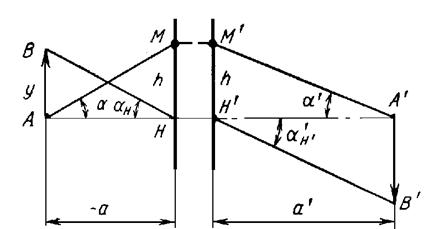
Рис. 18. 4.Угловое увеличение идеальной оптической системы.

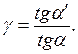
tg a = h/a; tg a` = h/a`.

Тогда

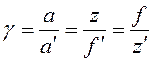. (18.5)

Или g = - f/f` 1/b.

В частном случае равенства переднего и заднего фокусных расстояний

bg = 1. (18.6)

Угловое увеличение в сопряжнных плоскостях равно обратному значению линейного увеличения.

Учитывая формулу (18. 4) находим:

a = b/g. (18.7)

Уравнение (инвариант) Лагранжа- Гельмгольца

На рис. 18.2. показан произвольный луч АМ, вышедший из точки А под углом a к оптической оси. Из рассмотрения треугольников АМН и A`D`H` находим:

H = a tga = a`tga`

или заменив а и а` отрезками z и фокусными расстояниями получим:

(z + f) tg a = (z` + f`) tg a`.

Подставив значения z и z` из (18.5) после упрощения получаем уравнение Лагранжа-Гельмгольца:

y f tga = - y` f` tga` или в параксиальном приближении:

n y a = n` y`a`. (18.8)

Инвариант Лагранжа-Гельмгольца справедлив для системы из произвольного числа преломляющих поверхностей. Он накладывает принципиальные ограничения на возможности оптических систем по «сжиганию на расстоянии».

Дата добавления: 2014-01-13